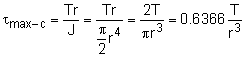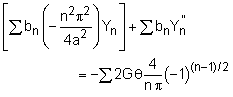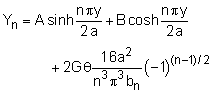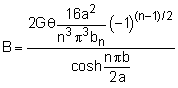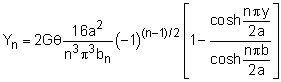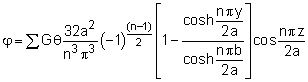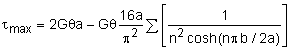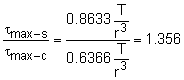| Ch 2. Torsion | Multimedia Engineering Mechanics | ||||||
|
Circular Bars |
Nonuniform & Indeterminate |
Thin-walled Tubes |
Non-Circular Bars | ||||
| Non-Circular Bars and Shafts | Case Intro | Theory | Case Solution |
| Chapter |
| 1. Stress/Strain |
| 2. Torsion |
| 3. Beam Shr/Moment |
| 4. Beam Stresses |
| 5. Beam Deflections |
| 6. Beam-Advanced |
| 7. Stress Analysis |
| 8. Strain Analysis |
| 9. Columns |
| Appendix |
| Basic Math |
| Units |
| Basic Mechanics Eqs |
| Sections |
| Material Properties |
| Structural Shapes |
| Beam Equations |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
|
|
||
|
|
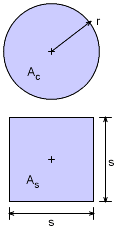
To compare the two bars, the area must be the same. Either the circular dimension, r, or the square dimension, s, can be used. This solution will use the r dimension in the calculations. Thus the circular bar cross sectional area, Ac is r2π. The square bar cross sectional area, As is s2. Since they need to be question, Ac = As => r2π = s2 Thus, s = π1/2 r = 1.7772 r |
|
| Circular Bar Maximum Shear Stress |
||
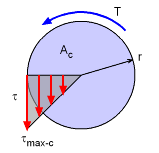 Maximum Shear Stress for Circular Bar |
The circular bar maximum stress can be easily determined using the basic shear stress equation derived in the circular bars section. |
|
| Rectangular Bar Shear Stress |
||
|
|
Rectangular bars is a simple geometry, but the solution is still lengthy since a second order partial differential equation must be solved. Recall, the equation that models all torsional shear stress is, where G is the shear modulus, θ is the angle (radians) of twist per unit length (not the total twist) and φ is the scalar stress function (used to find shear stress). |
|
 Rectangular Bar Cross Section Geometry |
To start, set the geometry to a width of 2a and a height of 2b as shown in the diagram. The dimension 'a' and 'b' are different for now, so the derived solution can be used for any rectangular shaped bar. The use of the z-axis pointing to the left is consistent with standard beam coordinates (x is along the beam center, or pointing out of the page in this case). Notice, the torsional shear stresses are only estimates in the diagram. Unlike a circular bar, the stresses will change for different location around the center. This makes the solution difficult (and lengthy). Like all solutions to differential equations, a trial solution is proposed, and then substituted back in to find a particular solution. Since the solution should be symmetrical around both the z-axis and y-axis, a cosine function should work. As a starting point, assume the stress function, φ, is |
|
where bn are constants (will cancel out later) and Yn are functions of 'y' that are not yet set. Now, substitute this assumed solution form back into the differential equation, giving All the terms on the left have cosine functions, but the right hand side does not. To make all terms consistent, the -2Gθ constant term can be written as a fourier series (basically just a series using sine and cosine) as |
||
This may seem complicated, but it will work out in the end. If the 2Gθ series is substituted into the previous equation, the cos terms will cancel, giving Where the ' (prime) marks represent derivatives with respect to y. Rearranging, moving bn term to the right hand side, and dropping the summation symbol for simplicity (still summing on all terms with n), gives |
||
Remember, the Yn terms are functions of y that have not yet been set. It will be done now. Basically, the equation above is another differential equation. The general solution is, Now the boundary conditions can be applied to determine the constants A and B. First, since the solution will be symmetrical about the z-axis, there can be no sinh term (anti-symmetric). Thus A must be zero. Next, B can be found with the boundary conditions φ = 0 at the edge, or when y = ±b, giving |
||
This give Yn as Substituting Yn ,back into the stress function, φ, gives Notice, the bn terms cancel. This is the full solution for the stress function at any point (y, z) for a rectangular cross section. |
||
But there are few more steps to make it useful for actual shear stresses. First is to take a derivative with respect to z to find the shear stress on the x-y plane, giving Likewise, the stress in the x-z plane can be found from τxz = dφ/dy. The total shear stress will be a combination of both the x-y and x-z plane stress. |
||
| Square Bar Maximum Shear Stress |
||
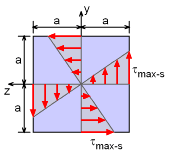 Square Bar Maximum Shear Stress |
The maximum shear stress will occur when z = ±a or y = ±b (depends if 'a' or 'b' is the long side). But for this problem, a = b, so it will not matter. Taking y = 0, and z = a, gives Notice, the sin term and the (-1)(n-1)/2 term will be both negative or both positive for the same n, so the final result will always be positive. This can be further simplified noting that Σ(1/n2) = π2/8 for n = 1, 3, 5, ... This gives, |
|
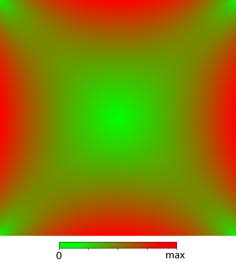 Square Bar Shear Stress Distribution |
This expression will converge quickly. Using only three terms (n = 1, 3, and 5), it is accurate to five significant digits. The result is, τmax-s = 1.3506 Gθa While the maximum is at the sides, it is interesting to note that the corners have zero shear stress as shown in the diagram. One last issue is the solution is in terms of G or θ, which are not given. The requires another equation relating Gθ with the applied torque, T. This can be done by summing both shear stresses over the cross sectional area. It can be shown (not given here) that summing the stress function, φ, over the domain, also gives the total torque, T. |
|
Completing this integration, and setting a = b, gives, T = 0.1406 Gθ (2a)4 or Gθ = 0.4445 T / a4 Substituting this back into the maximum shear stress equation, gives τmax-s = 0.6004 T / a3 Or in terms of the circular bar radius, r, where a = 0.5s and s = 1.7772 r, the maximum shear stress for the bar is τmax-s = 0.8633 T / r3 |
||
| Max Shear Stress Ratio for Square and Circular Bars |
||
The ratio of the maximum shear stress for the square bar to the circular bar (but with the same area) is, This means, the maximum shear stress in the bar is 35.6% higher than the circular bar. Unless the bars are at least 35% cheaper, it would not be wise to use the square bars. This is also why almost all drive shafts are round. |
||
Practice Homework and Test problems now available in the 'Eng Mechanics' mobile app
Includes over 500 free problems with complete detailed solutions.
Available at the Google Play Store and Apple App Store.