Torsional Scale

Front view of torsional scale

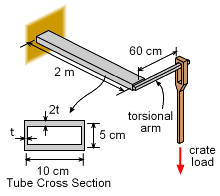
Say David, have you priced those heavy duty scales lately? They are extremely costly. There has to be a cheaper way to find the weight of these crates. David, you are the engineer, how about designing a simple torsional weighing system to find the weight of these heavy crates?

What is known:

• The thin-walled tube is 2 meters long.
• The torsional arm is 60 cm long.
• The tube is made from steel with a shear modulus, G, of 80 GPa.
• The shear stress limit of the steel, τ_max, is 350 MPa.
• The cross section of the tube is 10 cm by 5 cm as shown at the left.
• The tube wall thickness is not known but the top and bottom is twice the thickness of the sides.
• The torsional arm is stiff enough that it will not bend.
• The system should be able to weigh crates up to 12.5 kN.
• Assume the tube thickness is small when compared to the cross section dimensions and can be considered a thin-walled tube.
• Assume the applied moment due to the load is about the center of the tube and there is no out-of-plane twisting or deflection.

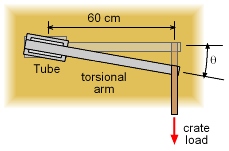
How thick should the tube walls be so the shear stress does not exceed the allowable limit? What is the relationship between the angle of twist, θ, and the weight of a crate hanging from the cable?

• The actual applied moment on the tube needs to be determined based on the torsional arm and the load.
• Before the angle of twist can be determined, the tube thickness on all sides needs to be calculated. This can be done using the shear flow equation for thin-walled tubes,
  
       
  
  and using the definition of shear flow,
  
       q = τ t
  
  
• The actual twist angle is related to the applied moment by using the angle of twist equation for thin-walled tubes,