| Ch 2. Torsion | Multimedia Engineering Mechanics | ||||||
|
Circular Bars |
Nonuniform & Indeterminate |
Thin-walled Tubes |
Non-Circular Bars | ||||
| Thin-walled Tubes | Case Intro | Theory | Case Solution | Example |
| Chapter |
| 1. Stress/Strain |
| 2. Torsion |
| 3. Beam Shr/Moment |
| 4. Beam Stresses |
| 5. Beam Deflections |
| 6. Beam-Advanced |
| 7. Stress Analysis |
| 8. Strain Analysis |
| 9. Columns |
| Appendix |
| Basic Math |
| Units |
| Basic Equations |
| Sections |
| Material Properties |
| Structural Shapes |
| Beam Equations |
| Search |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| Author(s): |
| Kurt Gramoll |
| ©Kurt Gramoll |
|
|
||
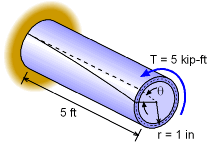 Thin-walled circular tube |
Example |
|
|
A simple 5 ft long circular steel tube is subjected to a torque (moment) of 5 kip-ft. The radius of the pipe (to the mid-point) is 1 inch and the wall thickness is 0.2 inch. What is the shear stress in the tube? Compare the shear stress based on theory developed in section "Circular Bars and Shafts" to the "Thin-walled Tube" theory developed in this section. |
||
| Solution |
||
 Circular tube Cross Section |
Shear Stress Based on Thin-walled Theory First, it is good to check if this is a thin walled tube. The thickness is 0.2 inches and the overall dimension of the tube is 2 inches. Thus, the thickness is roughly 10% of the overall cross section. This is on the border of being thin-walled. The solution should be assumed to be approximate, and not exact. The shear flow for a thin-walled tube is q = T/(2Ao) For this tube, the area is Ao = π rmid2 = π 12 = π in2 Thus, the shear flow is q = T/(2Ao) = (5 kip-ft)(12 in/ft)/(2 π in2) = = 9.549 kip/in The shear stress is τ = q/t = 9.549/0.2 = 47.75 ksi |
|
|
|
Shear Stress Based on Circular Bar Theory Shear stress based on circular bar theory is considered exact for circular bars and shafts. It will be interesting to see how well thin-walled theory compares. The shear stress for a circular bar is given by τ = Tro/J where J is the polar moment of inertia and ro is the outside radius. For this example, the polar moment of inertia is J = π ro4/2 - π ri4/2 = π [(1+0.2/2)4 - (1-0.2/2)4]/2 = 1.269 in4 Thus, the shear stress is τ = (5 kip-ft)(12 in/ft)(1.1 in) / (1.269 in4) = 52.01 ksi This is about 9% higher than the value calculated from thin-walled theory. Thus, for thin-walled theory to be accurate, the tube thickness should be less than 10% of the overall dimension. |
|
Practice Homework and Test problems now available in the 'Eng Mechanics' mobile app
Includes over 500 free problems with complete detailed solutions.
Available at the Google Play Store and Apple App Store.