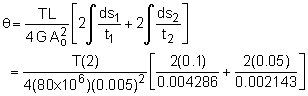| Ch 2. Torsion | Multimedia Engineering Mechanics | ||||||
|
Circular Bars |
Nonuniform & Indeterminate |
Thin-walled Tubes |
Non-Circular Bars | ||||
| Thin-walled Tubes | Case Intro | Theory | Case Solution | Example |
| Chapter |
| 1. Stress/Strain |
| 2. Torsion |
| 3. Beam Shr/Moment |
| 4. Beam Stresses |
| 5. Beam Deflections |
| 6. Beam-Advanced |
| 7. Stress Analysis |
| 8. Strain Analysis |
| 9. Columns |
| Appendix |
| Basic Math |
| Units |
| Basic Mechanics Eqs |
| Sections |
| Material Properties |
| Structural Shapes |
| Beam Equations |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
|
|
||
|
|
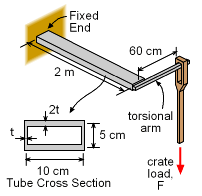
Due to the high cost of heavy duty scales, a simple but effective scale needs to be designed to weigh large crates. David, the lead engineer has decided to use a simple torsional scale using a thin-walled rectangular tube section. The tube is fixed to a wall at one end, and a stiff rod (torsional arm) is mounted at the other end as shown. The load is place at the far end of the rod, which produces a twisting moment or torque on the tube. This moment will then cause the tube to twist. The angle of twist will be proportional to the moment load. There are two unknowns in this problem. First, the actual thickness is not known. After the thickness is found, the actual angle of twist can be calculated for any given crate load, F. |
|
| Tube Thickness |
||
 Applied moment, T, on tube |
The moment, T, is produced by the weight of the crate acting over a distance of 60 cm, which is the length of the torsional arm. The maximum crate load is 12.5 kN, and thus the total maximum moment acting on the tube will be T = (0.60 m) (12.5 kN) = 7.5 kN-m The shear flow can be determined by using the shear flow equation, q = T/(2Ao) = 7.5/(2 [0.1][0.05]) = 750 kN/m The width and height is taken to the center of each wall. Recall, the maximum allowable shear stress was given as 350 MPa. This can be used to determine the minimum thickness of the tube. The thinnest edge is used to do the calculations since it will have the highest stress. |
|
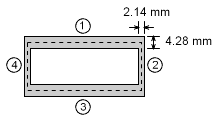
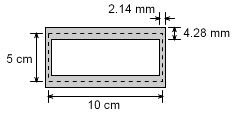 Final total thickness |
t = q/τ = (750 kN/m) / (350,000 kN/m2) = 0.002143 m = 2.143 mm Thus the left and right sides of the tube must be 2.143 mm thick to support a maximum crate weight of 12.5 kN. The top and bottom edges are twice as thick, with a total thickness of 4.2486 mm. The top and bottom edges will have a lower shear stress due to larger wall thickness. |
|
| Angle of Twist |
||
|
|
Now that the thickness is known, the angle of twist can be determined as a function of the moment, T. The angle is calculated by integrating around the circumference using, However, since the thickness is different on each edge, this equation must be integrated in parts as |
|
Since both sides 1 and 3, and sides 2 and 4 are equal, this can be simplified to = (0.00025) T (46.66 + 46.66) The angle of twist, θ, is related to the moment, T, as θ = 0.02333T radians, where the units of T are in kN-m. If the maximum load is applied, F = 12.5 kN, then the T will be 7.5 kN-m. This will give a maximum twisting angle of θ = 0.02333(7.5) = 0.1750 radians = 10.03o |
||
| It should be noted that this is an ideal situation. The tube and torsional bar will also undergo bending which will affect the angle of twist. Also, due to the large load on the thin-walled tube, the tube may buckle which is not covered in this section. | ||
Practice Homework and Test problems now available in the 'Eng Mechanics' mobile app
Includes over 500 free problems with complete detailed solutions.
Available at the Google Play Store and Apple App Store.