| Ch 2. Torsion | Multimedia Engineering Mechanics | ||||||
|
Circular Bars |
Nonuniform & Indeterminate |
Thin-walled Tubes |
Non-Circular Bars | ||||
| Circular Bars and Shafts | Case Intro | Theory | Case Solution | Example |
| Chapter |
| 1. Stress/Strain |
| 2. Torsion |
| 3. Beam Shr/Moment |
| 4. Beam Stresses |
| 5. Beam Deflections |
| 6. Beam-Advanced |
| 7. Stress Analysis |
| 8. Strain Analysis |
| 9. Columns |
| Appendix |
| Basic Math |
| Units |
| Basic Mechanics Eqs |
| Sections |
| Material Properties |
| Structural Shapes |
| Beam Equations |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
|
|
|||||
 Torsion of a Circular Bar |
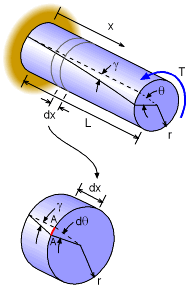
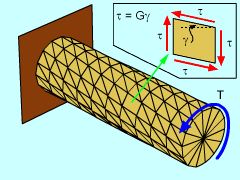
Torsion, like a linear force, will produce both stress and the strain. However, unlike linear stress and strain, torsion causes a twisting stress, called shear stress (τ), and a rotation, called shear strain (γ). The animation at the left illustrates as the torsion moment increases, the shear strain (angle γ) changes linearly. This concept will help develop equations that can be used to solve for the shear stress, strain and even the angle of twist. |
||||
| Torsional Stress and Strain |
|||||
|
|
If a torque (or moment) is applied to the end of a circular bar as shown, the bar will twist an angle θ. This angle will be a function of the bar length, L, and stiffness, G (shear modulus). The twist angle, θ, starts at 0 and increases linearly as a function of x. On the other hand, the change of angle, γ, is constant along the length. If a small differential element, dx, is sliced from the bar, the two angles must be compatible at the outside edge (arc length A-A in red). This gives the relationship, Arc Length A-A = r dθ = γ dx The change of angle, γ, is also the shear strain. Using Hooke's Law, the this angle is γ = τ/G Combining these two equations gives, τ = G r dθ/dx Generally, the rate of twist, dθ/dx, is not used but it is related to the torque, T. The following section will use this fact to develop a more useful form of this equation. |
||||
| Angle of Twist |
|||||
|
|
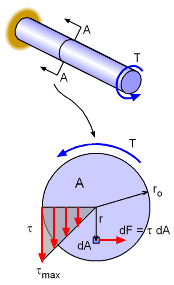
The first step is finding a relationship between the rate of twist, dθ/dx and the applied torque, T. From the previous equation, τ = G r dθ/dx, the shear stress is a linear function of the radius. The shear stress on all the differential elements, dA, generate a moment around the center, dM = r (τ dA) All these differential moments must total the applied moment or torque, T, giving Substituting the shear stress, τ, equations gives, Note that G and dθ/dx are constant, giving The integral term is a special form that is commonly seen in mechanic topics and has a special name, the polar moment of inertia, J. The equation for J depends only on the geometry and is commonly listed in engineering handbooks. Using the term J and rearranging, gives This can now be integrated along its length to find the total twist angle. If the torque, stiffness, and cross sectional area are constant, then this simplifies to
|
||||
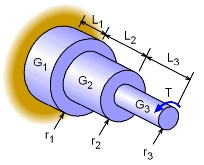 Angle of Twist for Shaft Constructed from Various Segments |
In cases when the circular shaft has different cross-sections along its length, the angle of twist equation can be applied on each section, and then summed.
Each segment can have a different load, length, stiffness and cross-section area. The total twist is simply the sum of all the individual segment twist angles. |
||||
| Torsional Shear Stress |
|||||
|
The equation for the rate of twist, dθ/dx = T/(GJ), can also be combined into the shear stress equation, τ = G r dθ/dx, to give the torsional shear stress as function of the radius. This simplifies to just,
This relationship assumes the G, J, and T are constant along the rod length. |
|||||
| Polar Moment of Inertia for Circular Rods |
|||||
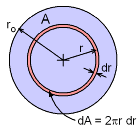 Polar Moment of Inertia Calculation |
Recall, the polar moment of inertia is defined as For a circular cross section, dA is the radius times the element thickness, giving dA = 2πr dr. Substituting into the integral gives, Solving gives,
|
||||
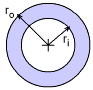 Polar Moment of Inertia for a Hollow Shaft |
This relationship can also be used for a hollow shaft. Simply use the outside radius, ro, to find the polar moment of inertia for a solid shaft, and then subtract the polar moment of inertia from the hollow section using the inside radius, ri. The relationship becomes, |
||||
If the difference between ro and ri is small, less than 5% of the ri, then the tube can be considered a thin-walled tube. The polar moment for thin tubes can be approximated by J = 2πr3t (t << r) where r is generally assumed to be the average radius of ro and ri. |
|||||
Practice Homework and Test problems now available in the 'Eng Mechanics' mobile app
Includes over 500 free problems with complete detailed solutions.
Available at the Google Play Store and Apple App Store.