| Ch 2. Torsion | Multimedia Engineering Mechanics | ||||||
|
Circular Bars |
Nonuniform & Indeterminate |
Thin-walled Tubes |
Non-Circular Bars | ||||
| Circular Bars and Shafts | Case Intro | Theory | Case Solution | Example |
| Chapter |
| 1. Stress/Strain |
| 2. Torsion |
| 3. Beam Shr/Moment |
| 4. Beam Stresses |
| 5. Beam Deflections |
| 6. Beam-Advanced |
| 7. Stress Analysis |
| 8. Strain Analysis |
| 9. Columns |
| Appendix |
| Basic Math |
| Units |
| Basic Mechanics Eqs |
| Sections |
| Material Properties |
| Structural Shapes |
| Beam Equations |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
|
|
||
|
|
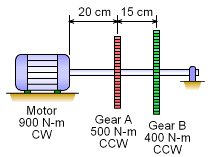
The motor generates 900 N-m torque (clockwise) which is transmitted to two gears. Each gear has a different moment load (counter-clockwise) as shown in the diagram. The shaft radius needs to be determined so that the maximum shear stress (τ = 275 MPa) is not exceeded. Also, there is a factor of safety of 2. The angle of twist can be calculated after the radius of the shaft is specified. The total twist will be the sum of each part of the shaft since the shaft moment is not constant from one end to the other. |
|
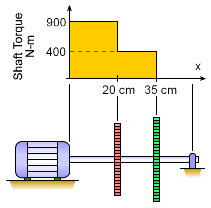
| Internal Moment in the Shaft |
||
|
|
The shaft radius needs to be large enough to withstand the largest moment. Thus, the first step is to identify the internal moment along the length of the shaft. The motor and gear moments are only input loads and not the actual internal shaft moments. The shaft from the motor to gear A has a constant moment of 900 N-m. However, from gear A to gear B, the moment in the shaft is reduced to only 400 N-m. Since there is no resisting moment at the right support, there will be no moment in the shaft from gear B to the the support. Thus, the largest moment is 900 N-m. |
|
| Shaft Radius |
||
|
|
The shaft must not exceed the yield stress of 275 MPa, including a factor of safety of 2.0. The radius can be determined using the torsion shear stress equation, The maximum stress will be half of 275 due to the factor of safety of 2.0. The polar moment of inertia, J, is also a function of the radius, J = (π/2) r4. Substituting, gives Solving for r gives, r = 0.01609 m = 1.609 cm |
|
| Angle of Twist |
||
|
The total angle of twist will be the sum of the rotation of each segment of the shaft. There are three segments, each with a different moment as given in the torque diagram above. The total twist angle is The shear modulus G, is same for all segments. Recall, G can be determined from E and ν. G = E/[2(1+ν)] = 69/[2(1 + 0.33)] = 25.94 GPa The polar moment of inertia, also the same in all segments, is J = (π/2) r4 = 1.571 (0.01609)4 = 1.0529× 10-7 m4 Combining, gives = 0.08787 radians Or in degrees, θtotal = 5.03o |
||
Practice Homework and Test problems now available in the 'Eng Mechanics' mobile app
Includes over 500 free problems with complete detailed solutions.
Available at the Google Play Store and Apple App Store.