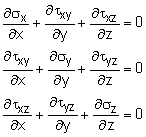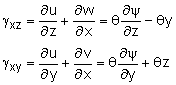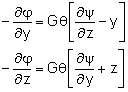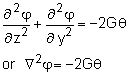| Ch 2. Torsion | Multimedia Engineering Mechanics | ||||||
|
Circular Bars |
Nonuniform & Indeterminate |
Thin-walled Tubes |
Non-Circular Bars | ||||
| Non-Circular Bars and Shafts | Case Intro | Theory | Case Solution |
| Chapter |
| 1. Stress/Strain |
| 2. Torsion |
| 3. Beam Shr/Moment |
| 4. Beam Stresses |
| 5. Beam Deflections |
| 6. Beam-Advanced |
| 7. Stress Analysis |
| 8. Strain Analysis |
| 9. Columns |
| Appendix |
| Basic Math |
| Units |
| Basic Mechanics Eqs |
| Sections |
| Material Properties |
| Structural Shapes |
| Beam Equations |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
|
|
|||||
| Torsion of Non-Circular Bars and Shafts |
|||||
|
|
There are cases when shafts or bars are not circular and must withstand a torque. In those cases, there are only a few closed form solutions, mainly elliptical, triangular, and rectangular shapes. For other type of shapes, a numerical method is needed. This section will develop the elasticity equations used to solve torsional shear stress for a rectangular bar. |
||||
| Elasticity Theory for Torsion |
|||||
|
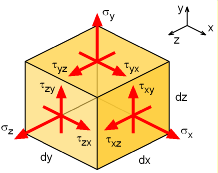
Torsional stress in non-circlular cross sections require using elasticity theory which, in general, is beyond the scope of this work. But for torsion, luckily, it is not too complex, and will presented here a basic introduction to Elasticity. First, stresses in all three directions need to be defined. There are three normal and three shear stresses for each face of a typical stress cube as shown in the figure. The material is assumed, isotropic, thus, τxy = τyx, τxz = τzx, and τyz = τzy. Summing forces in each of the three directions over the differential distance of dx, dy and dz gives the following general 3D equilibrium equations, Since there are six unknowns but only three equations, additional equations (compatibility relationships) are required or the number of unknowns need to be reduced. |
||||
|
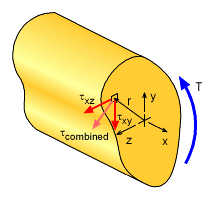
For pure torsion about the x-axis, the equilibrium equations above can be simplified to one equation since σx = σy = σz = τyz = 0, giving, Notice, there are two direction for the shear stress on the y-z plane, in the direction of the y-axis (τxy) and one in the direction of the z-axis (τxz). To simplify the solution derivation, it is common to use a new scalar function, φ, in place of the stress terms. Mathematically, it is possible to let the two unknown stresses be a function of this arbitrary scalar function, so that If these two relationships are substituted into the previous equilibrium equation, the result is zero which verifies they are mathematically correct. However, the scalar function, φ, is of higher order, and additional boundary conditions are needed. |
||||
Next, the strain compatibility equations are needed since elasticity theory is basically indeterminate structural analysis in 3D. There will be a total of six strain relationships, where four of them are equal to zero, giving The three normal strains (εx, εy, εz) are zero since only a torque load, T, is a applied about the x-axis. Also, the y-z plane shear (γyz) will be zero. However, the shear in the x-z and x-y planes will be non-zero and will vary depending on the y and z location, as shown in the diagram above. |
|||||
The in-plane displacements functions, v and w will be functions of both location (x, y, z) and the unit angle of twist, θ, such as v = θ x z The derivation of the above relationship can be done by taking a small angle rotation, Δθ, and assume some displacements. Note, θ is the twist angle per unit length and not the total twist. The u function is the out-of-place displacements. It can be modeled a warping function, ψ(y,z) and the twist angle, θ, u = θ ψ(y,z) The warping function does not actually need to be known to find the shear stresses. In fact, it will be eliminated later by canceling terms. Continuing, the displacement functions, u, v, and w, are now substituted back into the two strain equations, giving, |
|||||
The final step is using Hooke's law to relate the stress terms with the strain terms, τxz = G γxz Substituting the scalar function, φ, for stresses and warping function, ψ, (and twist angle, θ) for strains, gives, To eliminate the warping function, ψ, take a derivative of the first equation with respect to y and a derivative of the second equation with respect to z, and then subtract the two equation. This gives
Again, the scalar function, φ, is a just a mathematical construct to help solve the actual stress. Once φ is found, then the derivative with respect to z and y will give the shear stresses, as To solve for φ, the boundary condition needs to be known. For solid torsional bars, the outside edge has zero shear stress, so φ must be a constant at the edge. For convenience, that value of φ is set to zero on the boundary. In the section below, this equation is solved for a solid rectangular bar. But for most geometries, there is no closed for solution. However, since the equation is actually the Poisson's equation, it can be easily solved using numerous numerical methods such as finite element method. |
|||||
| Torsion Solver Tool |
|||||
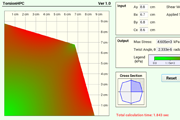 2D Torsion Stress Tool - Torsion HPC |
For non-circular and non-rectangular bars, a basic numerical solver has been developed. The Torsion Stress Analysis Tool can be used on any mobile device for free. For Android mobile devices, "Torsion HPC", can be downloaded at Google Play. For iOS (Apple) mobile devices, "Torsion HPC", can be downloaded at iTunes.
|
||||
Practice Homework and Test problems now available in the 'Eng Mechanics' mobile app
Includes over 500 free problems with complete detailed solutions.
Available at the Google Play Store and Apple App Store.