| Ch 2. Particle Force and Acceleration | Multimedia Engineering Dynamics | ||||||
|
Rect. Coord. |
Normal/Tang. Coord. |
Polar Coord. |
Orbital Mechanics | Computational Mechanics | |||
| Rectangular Coordinates | Case Intro | Theory | Case Solution | Example |
| Chapter |
| - Particle - |
| 1. General Motion |
| 2. Force & Accel. |
| 3. Energy |
| 4. Momentum |
| - Rigid Body - |
| 5. General Motion |
| 6. Force & Accel. |
| 7. Energy |
| 8. Momentum |
| 9. 3-D Motion |
| 10. Vibrations |
| Appendix |
| Basic Math |
| Units |
| Basic Dynamics Eqs |
| Sections |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
|
|
|||||
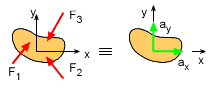 Free-Body Diagram (FBD) and Mass-acceleration Diagram (MAD) are Directly Related |
Newton's Second Law states that the force on a particle is equal to the rate of change of its linear momentum, or F = d(mv)/dt Sometimes, linear momentum, L, is given as L = mv If the mass is constant, then the more familiar force equation is derived, This relationship basically states non-equibilirium forces will cause the object to accelerate. This a the core concept in dynamics and most problems will require its use, regardless of coordinate system. To help set up problems, it is often useful to construct both a free-body diagram and a mass-acceleration diagram to represent each side of the equation. They can also be combined showing both the forces and acceleration vectors on the same diagram. |
||||
A large body, such as a car, plane, or boat, can be considered a particle for the purpose of analyzing its motion, provided the effects of rotation about the center of mass can be ignored (rigid body rotation is addressed in later chapters). The total force and acceleration acting on a particle can be expressed in terms of rectangular components. This can be broken down into 3 scalar equations. ΣFx = max |
|||||
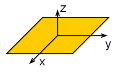 Motion in the x-y Plane |
Plane Motion |
||||
|
If the motion of a particle is confined to the x-y plane, then the totalforce in the z direction is zero. ΣFz = 0 |
|||||
| Line Motion |
|||||
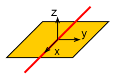 Motion along a Line in the x direction |
If a particle travels along a straight line, then the sum of forces perpendicular to that line is zero. ΣFy = 0 ΣFz = 0 |
||||
Practice Homework and Test problems now available in the 'Eng Dynamics' mobile app
Includes over 400 free problems with complete detailed solutions.
Available at the Google Play Store and Apple App Store.