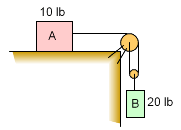
Two different blocks are connected through a pull system and released. What is tension in the cable? The coefficient of static and kinetic friction between block A and the ground is 0.4 and 0.25, respectively. Assume the pulley is massless and frictionless.

Check if Blocks are in
Static Equilibrium

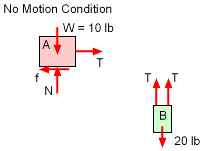
Two actions can take place with this system. First, the coefficient of static friction is sufficient to keep the block from moving (No Motion Condition). This situation will occur when

     f ≥ T

The tension in the cable is simply half the weight of block B, or 10 lb. The friction force, f, will be μN, or 0.4(10 lb) = 4 lb. Thus, f is not larger than the tension, and the blocks will move. This is not surprising since this is a dynamics course.

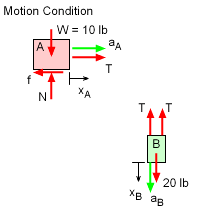
Since the blocks will move, each will have an acceleration that directly affects the cable tension. Free-body diagrams with acceleration vectors for each block helps organize all actions affecting the blocks. Summing forces and accelerations give
     Block A:  T - f = a_Am_A
     Block B:  20 - 2T = a_Bm_B

The friction is simply N = 0.25(10) = 2.5 lb using the kinetic coefficient of friction. But the acceleration terms need to be related to reduce the unknowns to just two.

The pulley effectively reduces the motion of B to half the motion of A, or in equation form,
      x_B = 0.5x_A

This can be integrated twice to give,
     a_B = 0.5a_A

Substituting known information into basic equations give,
     Block A:  T - 2.5 = a_A (10/g)
     Block B:  20 - 2T = 0.5a_A (20/g)

Combining,
     20 - 2T = 0.5 [(T - 2.5) (g/10)] (20/g)
     20 - 2T = T - 2.5
     22.5 = 3T

Solving gives,

T = 7.5 lb

It is interesting to note, if there was no friction, the equation becomes,

     20 - 2T = 0.5 [(T - 0) (g/10)] (20/g)
     20 = 3T

or T_{no friction} = 6.667 lb