| Ch 2. Particle Force and Acceleration | Multimedia Engineering Dynamics | ||||||
|
Rect. Coord. |
Normal/Tang. Coord. |
Polar Coord. |
Orbital Mechanics | Computational Mechanics | |||
| Rectangular Coordinates | Case Intro | Theory | Case Solution | Example |
| Chapter |
| - Particle - |
| 1. General Motion |
| 2. Force & Accel. |
| 3. Energy |
| 4. Momentum |
| - Rigid Body - |
| 5. General Motion |
| 6. Force & Accel. |
| 7. Energy |
| 8. Momentum |
| 9. 3-D Motion |
| 10. Vibrations |
| Appendix |
| Basic Math |
| Units |
| Basic Equations |
| Sections |
| Search |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| Author(s): |
| Kurt Gramoll |
| ©Kurt Gramoll |
|
|
||
| Solution of a) - Horizontal Belt |
||
|
|
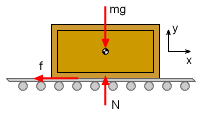
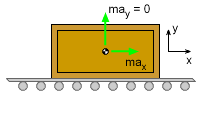
Begin with a free-body diagram (FBD), which shows the forces acting on the crate, and a mass-acceleration diagram (MAD), which shows the inertia vector of the crate. Since there is no force in the z direction, the motion is confined to the x-y plane. Using Newton's Second Law, sum the forces in both directions. Note that there is no acceleration in the y direction. ΣFy
= may In the x direction, the sum of the force are ΣFx = -f = max |
|
The friction force depends on the static coefficient of friction (no motion) to start moving, f = μs N = μs mg The equations can be combined to give an expression for ax in terms of μs, -μs mg = max |
||
|
Divide both sides by m, ax = dv/dt = -μs g Then Integrate ax to find an expression for v, An expression for x(t) can be found by integrating v(t), Knowing that vo = 10 ft/s, the expression for v(t) can be used to find the time required for the belt to come to a stop, v(t) = 0 = -μsgt
+ 10 Substituting the time into the x(t) function gives the minimum distance to stop, x = 10 (0.6211) -1/2 (0.5)(32.2)(0.6211)2 |
|
| Solution of b) - Inclined Belt |
||
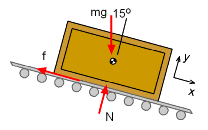 Free-body Diagram (FBD)
|
As with all dynamic problems, it is best to start with a free-body and a mass-acceleration diagrams. These are shown at the left for this problem. First, rotate the x-y axis to be parallel and perpendicular to the conveyor belt. This will simplify calculations. Using Newton's Second Law, sum the forces in both directions. Noting that there is no acceleration in the y direction, these equations become ΣFy = may In the x direction, ΣFx = max The friction force in terms of μs and g is f = μs N = μs mg cosθ Combining equations, and dividing through by m gives an expression for ax in terms of μs. ax = dv/dt = g sinθ - μs g cosθ> |
|
|
Integrating ax gives an expression for v, Now the next step can be taken by integrating the velocity function to find the position function. v(t) = dx/dt Integrating v(t) gives x(t) as Knowing that vo = 10 ft/s, the time required for the belt to come to a stop is t (32.2) (sin15 - 0.5 cos15) = -10 Substitute the time into the expression for x(t) gives the minimum distance to stop, x = 1/2 (32.2)(1.386)2 (sin15 - 0.5cos15)
+ 10(1.386) |
|
|
||
Practice Homework and Test problems now available in the 'Eng Dynamics' mobile app
Includes over 400 free problems with complete detailed solutions.
Available at the Google Play Store and Apple App Store.