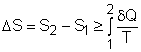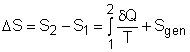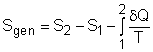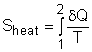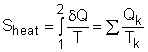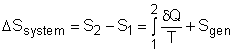| Ch 6. Entropy | Multimedia Engineering Thermodynamics | ||||||
| Entropy | Tds Relations |
Entropy Change |
Isentropic Process |
Isentropic Efficiency |
Entropy Balance (1) |
Entropy Balance (2) |
Reversible Work |
| Entropy Balance | Case Intro | Theory | Case Solution |
| Chapter |
| 1. Basics |
| 2. Pure Substances |
| 3. First Law |
| 4. Energy Analysis |
| 5. Second Law |
| 6. Entropy |
| 7. Exergy Analysis |
| 8. Gas Power Cyc |
| 9. Brayton Cycle |
| 10. Rankine Cycle |
| Appendix |
| Basic Math |
| Units |
| Thermo Tables |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
| |
|||||||||
| Entropy Generation |
|||||||||
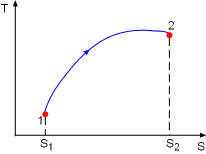 Process 1-2 on T-s Diagram |
Consider a system undergoing a process 1-2 as shown in the diagram.The increase of entropy principle states The above equation can be expressed as |
||||||||
|
where Sgen is called entropy generation. Sgen measures the effect of irreversibilities present within the system during a process. Its value depends on the nature of the process and not solely on the start and end states. Hence, it is not a property. Rewriting the above equation gives the expression of entropy generation as According to the
increase of entropy principle, entropy generation can
only take a non-negative value. |
||||||||
| Entropy Balance
|
|||||||||
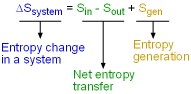 Entropy Balance for a System |
The entropy balance is an expression of the second law of thermodynamics that is particularly convenient for thermodynamic analysis. The increase of entropy principle states that the entropy can only be created, and it is expressed as (Entropy change in a system) or ΔSsystem = Sin - Sout + Sgen This expression is the entropy change of a system. It is applicable to any system undergoing any process. In unit-mass basis, it is Δssystem = sin - sout + sgen The first and second terms in the right hand side of the
equation represent the entropy transfer between the system and its surroundings.
The
third term represents the entropy generation in the
system. |
||||||||
| Entropy Transfer
|
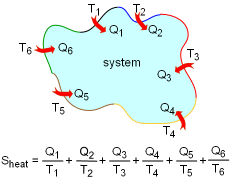 Entropy Transfer by Heat with Different Boundary Temperatures |
Entropy can be transferred to or from a system by two mechanisms: heat transfer and mass flow. Note that no entropy is transferred by work. Heat Transfer Heat transfer to a system increases the entropy of the system, and heat transfer out of a system decreases the entropy of the system. During a process 1-2 of a system as defined above, If heat transfer δQ happens at the system boundary which has an absolute temperature T, the entropy transfer associated with this heat transfer process is If the entire boundary temperature remains as a constant T, the above equation can be simplified as Sheat = Q/T where When the temperature T is not a constant, but a function of its location, the entropy change can be approximated as where |
|||||||
|
|
Mass Transfer Mass contains entropy as well as energy. Mass m, which has a specific entropy s, contains a total entropy of ms. When a mass flows in a system, the entropy increase in the system is ms. In the same manner, mass m flowing out of a system will result in a decrease of entropy in amount of ms in the system. Smass = ms |
||||||||
| Entropy Balance for Closed Systems |
|||||||||
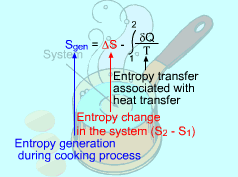 Consider the Egg as a Closed System |
A closed system involves no mass transfer between the system and its surroundings, and thus its entropy transfer is only from heat transfer. If the closed system undergoes an adiabatic process, then no heat transfer occurs at the boundary. The entropy balance is reduced to |
||||||||
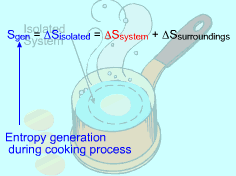 Consider the Isolated System Formed by the Egg and the Surrounding Water |
A system and its surroundings forms an isolated system. The entropy change of an isolated system formed by a closed system and its surroundings is ΔSisolated = ΔSsystem + ΔSsurr = Sgen
|
||||||||