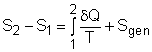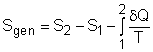| Ch 6. Entropy | Multimedia Engineering Thermodynamics | ||||||
| Entropy | Tds Relations |
Entropy Change |
Isentropic Process |
Isentropic Efficiency |
Entropy Balance (1) |
Entropy Balance (2) |
Reversible Work |
| Entropy Balance | Case Intro | Theory | Case Solution |
| Chapter |
| 1. Basics |
| 2. Pure Substances |
| 3. First Law |
| 4. Energy Analysis |
| 5. Second Law |
| 6. Entropy |
| 7. Exergy Analysis |
| 8. Gas Power Cyc |
| 9. Brayton Cycle |
| 10. Rankine Cycle |
| Appendix |
| Basic Math |
| Units |
| Thermo Tables |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
|
|
||
|
Entropy generated by cooking an egg from 10oC to 100oC in boiling water needs to be determined. Assumptions:
|
||
 Consider the Egg as a Closed System |
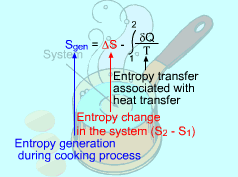
(1) Method A: Consider the egg as a closed system Take the egg as a system. It is a closed system since no mass flow in or out of the egg. The entropy balance for a closed system is: Rearranging the above equation gives the expression of the entropy generation. That is, The first two terms on the right hand side of the above equation corresponds to the entropy change in the system, and the third term is the entropy transfer by heat. The entropy change in the system: The egg is approximated as an incompressible substance. With constant-specific-heat assumption, its entropy change can be determined from ΔS = S2 - S1 = mCaveln(T2/T1) where 1 denotes the initial state and 2 denotes the final state. Hence, T1 = 10 oC = 283 K The mass of the egg is m = Vρ = 4/3(3.14)(0.03)3(1000) = 0.113 kg The average specific heat is given as 3.4 kJ/(kg-K). Substituting all the data into the expression of entropy change yields S2 - S1 = 0.113(3,400) ln(373/283) = 106.1 J/K The entropy transfer to the egg by heat: The egg is cooked from 10oC to 100oC in 100oC water. Assume the boundary of the egg remains 100oC during the whole process and hence the entropy transfer to the egg by heat transfer can be determined by where Q is the heat transferred to the egg from the surrounding water, and T is 100oC. Q can be determined by the energy balance of the egg. Q - W = U2 - U1 Substituting Q and T to the expression of entropy transfer gives, Q/T = 34,578/(373) = 92.7 J/K After calculating the entropy change in the system and the entropy transfer by heat, the entropy generation can be determined. It is Sgen = (S2 - S1) - Q/T |
|
|
|
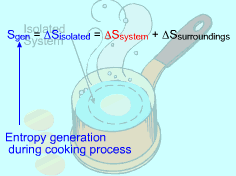
(2) Method B: Consider the isolated system formed by the egg and the water surrounding it First, consider the egg as a system. Then the egg and the surrounding water as an isolated system. The entropy generated during the cooking process equals the entropy change of the isolated system. Sgen = ΔSisolated = ΔSsystem + ΔSsurroundings The entropy change of the system has been calculated in method A, which is ΔSsystem = 106.1 J/K Consider the surrounding water. The water remains 100 oC in the entire process. Hence, ΔSsurroundings = Q/T where Q equals the heat transferred to the system in value but has negative sign, which indicates that heat is transferred from the water. Q = -34,578 J The entropy change in the surrounding water is Q/T = -34,578/373 = - 92.7 J/K Summing up the entropy change in the system and the entropy change in the surrounding water yields the entropy generation during the egg cooking process. That is, Sgen = 106.1 - 92.7 = 13.4 J/K The result obtained is the same as that in method A. |
|