| Ch 8. Internal Loads | Multimedia Engineering Statics | ||||||
|
Int. Forces and Moments |
V and M Diagrams I | V and M Diagrams II | V, M, Load Relationships | ||||
| Internal Forces and Moments | Case Intro | Theory | Case Solution |
| Chapter |
| 1. Basics |
| 2. Vectors |
| 3. Forces |
| 4. Moments |
| 5. Rigid Bodies |
| 6. Structures |
| 7. Centroids/Inertia |
| 8. Internal Loads |
| 9. Friction |
| 10. Work & Energy |
| Appendix |
| Basic Math |
| Units |
| Sections |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
|
|
||
 Free Body Diagram |
Form a free-body diagram and solve for the external reactions giving, ΣMA = 0 ΣFy =
0 |
|
| Solution of Internal Forces |
||
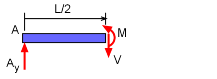 Left Section |
If the beam is cut just to the left of the applied load, then the proper free-body diagram for the section to the left of the cut is as shown. Notice, it does not include the 300 lb force since it is cut just before the force. Sum the forces and moments to solve for the unknown internal loads: ΣFy
= 0 ΣMA = 0 |
|
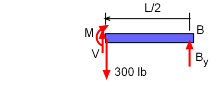 Right Section |
The problem can also be solved by using the right section after making the cut. The free-body diagram for the right side section is as shown at the left. Notice, the 300 lb force is included on this section since the cut is to the left of the force. Summing the forces and moments give, ΣFy = 0 ΣMB = 0 As expected, both methods obtain the same results, a shear force of 150 lb and a bending moment of 600 lb-ft. |
|
Practice Homework and Test problems now available in the 'Eng Statics' mobile app
Includes over 500 free problems with complete detailed solutions.
Available at the Google Play Store and Apple App Store.