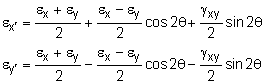| Ch 8. Strain Analysis | Multimedia Engineering Mechanics | ||||||
|
Plane Strain |
Mohr's Circle for Strain |
Strain Gages |
|||||
| Plane Strain and Principal Strains | Case Intro | Theory | Case Solution | Example |
| Chapter |
| 1. Stress/Strain |
| 2. Torsion |
| 3. Beam Shr/Moment |
| 4. Beam Stresses |
| 5. Beam Deflections |
| 6. Beam-Advanced |
| 7. Stress Analysis |
| 8. Strain Analysis |
| 9. Columns |
| Appendix |
| Basic Math |
| Units |
| Basic Mechanics Eqs |
| Sections |
| Material Properties |
| Structural Shapes |
| Beam Equations |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
|
|
||
 Strain Element |
Example |
|
|
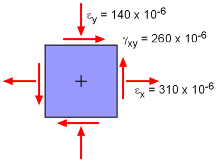
What is the largest principle strain for the strain element shown on the left? |
||
| Solution |
||
|
The given strain components are, εx = 310×10-6 =
310 μ where m represents micro-strains. |
||
The principal strain equations could be used directly, but another way is to find the principal angles, and then use them to find the principal strains. The principle angles for this strain state are tan 2θp = γxy /
(εx - εy) |
||
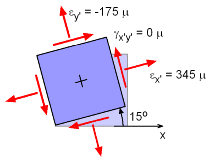 Rotated Strain Element, 15° |
Notice there are two possibilities. Both will give the same principal strains as will be shown below. For 15o, the two normal strains are, εx' = [310 + (-140)] / 2
+ [310 - (-140) ] / 2 cos30 εy' = [310 + (-140)] / 2
- [310 - (-140)] / 2 cos30 The principal strains are, ε1 = εx' = 344.9 μ @
15°
|
|
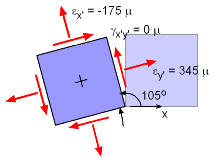 Rotated Strain Element, 105° |
The other angle,
105°, will give the same results, but x' and y' will be reversed.
εx' = [310 + (-140)] / 2
+ [310 - (-140)] / 2 cos210 εy' = [310 + (-140)] / 2
- [310 - (-140)] / 2 cos210 The principal strains are, ε1 = εy' = 344.9 μ @
105° As expected, the principal strain values are the same, the new coordinate, x' and y' are just reversed. But actually, the direction are the same sine this angle is 90 degree off from the previous angle. |
|
Practice Homework and Test problems now available in the 'Eng Mechanics' mobile app
Includes over 500 free problems with complete detailed solutions.
Available at the Google Play Store and Apple App Store.