| Ch 5. Beam Deflections | Multimedia Engineering Mechanics | ||||||
|
Integration of Moment |
Integration of Load |
Method of Superposition |
Indeterminate Beams |
||||
| Indeterminate Beam Structures | Case Intro | Theory | Case Solution | Example |
| Chapter |
| 1. Stress/Strain |
| 2. Torsion |
| 3. Beam Shr/Moment |
| 4. Beam Stresses |
| 5. Beam Deflections |
| 6. Beam-Advanced |
| 7. Stress Analysis |
| 8. Strain Analysis |
| 9. Columns |
| Appendix |
| Basic Math |
| Units |
| Basic Mechanics Eqs |
| Sections |
| Material Properties |
| Structural Shapes |
| Beam Equations |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
|
|
||
| Introduction |
||
|
|
Previously, indeterminate structures were presented for uniaxial and torsional loaded members. The same method can also be used for indeterminate beam structures. Mainly, redundant supports are removed and replaced with unknown reaction forces. Then additional equation(s) from compatibility conditions are used to solve for the extra unknown reaction forces. The beam load-deflection equation can also be integrated to give the deflection equations for each span or section. This is a bit more tedious since four boundary conditions are needed for each span. |
|
| Basic Indeterminate Beams |
||
|
|
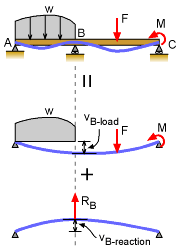
The most common indeterminate beam is when there just one redundant support. For example, the simple supported beam at the left has a redundant support at B (could also state A or C is redundant, but it is generally easier to solve if the middle support is considered redundant). The solution method is to release the redundant support and find the deflection at the support location. This can be done using beam deflection equations in handbooks (see Beam Equations Appendix) or basic integration of the moment or load-deflection equation. Next, without the loads, place the unknown redundant reaction force on the beam and find the deflection at the support location in terms of the unknown reaction. Finally, apply the compatibility equation. Generally, this will be the deflection at the released support must equal the deflection due to the reaction force. In the case of the example at the left, this would be vB-load = vB-reaction This equation will only have one unknown, RB which can now be determined. Once the redundant reaction forces are known, then the static equations can be used to find the other reaction forces. And then, with all the reaction forces known, the deflection at any point can be found using the principle of superposition. |
|
| Second Order Indeterminate Beams |
||
 Second Degree Indeterminate Beam |
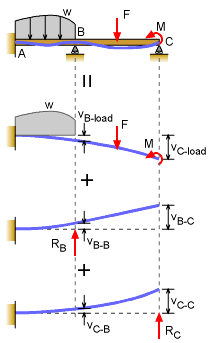
If there are two redundant supports, then the beam is indeterminate to the second degree. If there are three redundant supports, then it is a third degree indeterminate beam (and so forth). For example, the beam at the left could be considered a cantilever beam with two redundant supports. This is an indeterminate beam to the second degree. To solve the problem, release two redundant supports. It does not matter which supports are released, but there are generally better ones than others. The key is to have a basic beam that is listed in the appendix with beam equations. The beam without the redundant supports can be solved for the deflection at each support location. Usually, beam equation tables are used, similar to the ones listed in the Beam Equation appendix. But integration method could also be used. Next, one at a time, place the two unknown reaction forces on the cantilever beam. In this case, RB and RC are unknown reactions. Each unknown reaction causes a deflection at both support locations. The final step (and the key to solving indeterminate beams) is to apply the compatibility equation(s). There must be one compatibility equation per redundant support. In this case, there are two, giving vB-load = vB-B + vC-B vC-load = vB-C + vC-C where vB-B is the deflection at B due to the unknown reaction at B and vC-B is the deflection at B due to the unknown reaction at C. Similarly, vC-C is the deflection at C due to the unknown reaction at C and vB-C is the deflection at C due to the unknown reaction at B. All these terms will have one of the two unknowns, RB and RC, in there expressions. The deflection due to all loads are vB-load and vC-load. There will be two equations, and two unknowns. For each indeterminate degree, there will be one equation and one unknown. |
|
| Integrating Load-Deflection Equation to solve Indeterminate
Structures |
||
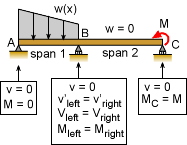 Boundary Conditions for Indeterminate Beam with Redundant Support (note, Slope = v´ = dv/dx = θ, and Shear = V) |
In addition to using superposition to solve for redundant supports, the basic load-deflection equation can be integrated to find the deflection. This method is the same technique used to determine the deflection equation for statically determinate beams. This method is tedious due to the large number of boundary conditions required. However, at times it can be useful when a deflection equation is needed, instead of the the reaction forces or deflection at a given location. For each span or section, four boundary conditions are needed. They can be deflection, v, slope, dv/dx or θ, shear, V, or moment, M. Each load or support change will require a new span. The basic load-deflection equation, EIv´´´´ = -w(x) must be integrated four times for each span or beam section. The constants of integration are determined from the boundary conditions. A summary of the common boundary conditions are listed below (from Integration of Load Equation section.) |
|
 Typical Boundary Conditions (v, v´, V, M) for Beam Sections Using Fourth Order Load-Deflection Equation |
||
Practice Homework and Test problems now available in the 'Eng Mechanics' mobile app
Includes over 500 free problems with complete detailed solutions.
Available at the Google Play Store and Apple App Store.