| Ch 1. Stress and Strain | Multimedia Engineering Mechanics | ||||||
|
Normal Stress |
Shear and Bearing Stress |
Normal Strain |
Hooke's Law |
Thermal Effects |
Indeterminate Structures |
||
| Indeterminate Axial Structures | Case Intro | Theory | Case Solution | Example |
| Chapter |
| 1. Stress/Strain |
| 2. Torsion |
| 3. Beam Shr/Moment |
| 4. Beam Stresses |
| 5. Beam Deflections |
| 6. Beam-Advanced |
| 7. Stress Analysis |
| 8. Strain Analysis |
| 9. Columns |
| Appendix |
| Basic Math |
| Units |
| Basic Mechanics Eqs |
| Sections |
| Material Properties |
| Structural Shapes |
| Beam Equations |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
|
|
||
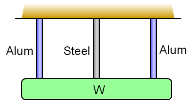 Simple Indeterminate Structure |
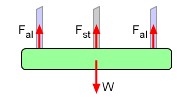
An indeterminate structure is when there are more reactions or supports than are needed to keep the structure in static equilibrium. As an example, an objected supported by three rods, as shown on the left, is indeterminate to the first degree, i.e. there is one redundant support. If it is redundant, why are indeterminate structures used? They help distribute loads to more supports which can reduce individual loads and moments. A general explanation of indeterminate structures can be found in the Indeterminate Objects section of the Statics eBook. |
|
| Stress and Deflection Superposition |
||
|
|
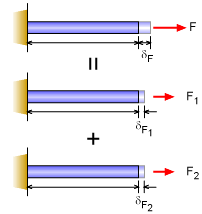
A useful concept in solving indeterminate structures is the Principle of Superposition. Simply stated, a problem can be reduced to smaller problems and the solutions to the smaller problems can be added together to give the solution to the original problem. This can be better understood by considering the deflection of a rod with two forces as shown in the diagram. This problem can be reduced to two separate problems, each with one force. The deflection of the rod due to each individual load is calculated. The the total deflection of the rod is simply the total of the two separate deflections. In equation form, F = F1 + F2 δF = δF1 + δF2 This is a simple problem, but it serves as the basis for superposition. The solution of individual problems can be superimposed to give the combined solution. It also works for stress calculations. It can even be used for thermal expansion. This concept does have limits. It can only be used when the material responds in a linear fashion (true for all problems in basic solid mechanics). This idea will be used many times in the future. |
|
| Indeterminate Axial Structures |
||
|
|
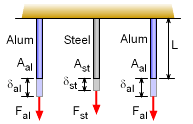
Structures that have too many supports are classified as indeterminate structures. This section examines only 1D or axial indeterminate structures where all displacements occur in the same direction. An example of this is a weight supported by three rods as shown on the left. Equilibrium Equation(s) For the given example, the equilibrium equations can relate the rod forces to the weight of the weight. This gives 2Fal + Fst = W (example equilibrium) However, the exact force in either rod cannot be determined with just the equilibrium equations. |
|
|
|
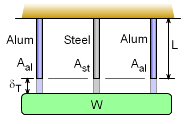
Compatibility Equation(s) Continuing with the example with three rods, compatibility condition requires that all deflections are the same. If there was no constraint (the weight) then each rod would deflection differently as shown in the diagram on the left. However, all the deflections are constrained by the weight, so they have the same deflection, |
|
|
|
δT = δal = δst (example compatibility) This condition is indicated in the diagram on the left. This relationship is only valid for this example and other problems will have different relationships. Combining Equations |
|
|
Simplifying gives, Substituting into the equilibrium equation gives, The force in the steel rod can now be determined. While other problems will use different compatibility equations the solution process is the same. If the structure has more than one redundant support, then more compatibility equations are needed. For each redundant support, a separate compatibility equation is needed. |
||
Practice Homework and Test problems now available in the 'Eng Mechanics' mobile app
Includes over 500 free problems with complete detailed solutions.
Available at the Google Play Store and Apple App Store.