| Ch 1. Stress and Strain | Multimedia Engineering Mechanics | ||||||
|
Normal Stress |
Shear and Bearing Stress |
Normal Strain |
Hooke's Law |
Thermal Effects |
Indeterminate Structures |
||
| Indeterminate Axial Structures | Case Intro | Theory | Case Solution | Example |
| Chapter |
| 1. Stress/Strain |
| 2. Torsion |
| 3. Beam Shr/Moment |
| 4. Beam Stresses |
| 5. Beam Deflections |
| 6. Beam-Advanced |
| 7. Stress Analysis |
| 8. Strain Analysis |
| 9. Columns |
| Appendix |
| Basic Math |
| Units |
| Basic Mechanics Eqs |
| Sections |
| Material Properties |
| Structural Shapes |
| Beam Equations |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
|
|
||
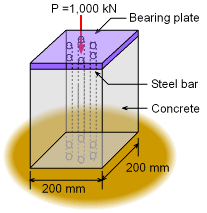 Reinforced Concrete Post |
Example |
|
|
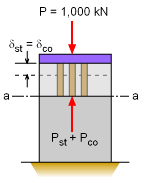
A short concrete post is reinforced with six symmetrically placed steel bars so that it can carry a load, P, of 1,000 kN. The concrete post is 200 mm by 200 mm and the cross-sectional area of steel bars is circular. If the allowable stresses of the steel, σst, and concrete, σco, are 120 MPa and 6 MPa, respectively, what is the minimum diameter of the steel bars? Assume the modulus of elasticity of the steel, Est, and and concrete, Eco, are 14 GPa and 200 GPa, respectively. |
||
| Solution |
||
|
The applied load, P, will be distributed between the steel and the concrete. From equilibrium at an arbitrary section a-a, these forces can be correlated as To determine the correct amount of steel required, first assume the concrete will reach it allowable stress limit of 6 MPa. This gives, σst = 14.29 (6) The total cross-sectional area, Ast, is the total of the six steel bars. Thus, the area of a single steel bar will be |
|
Practice Homework and Test problems now available in the 'Eng Mechanics' mobile app
Includes over 500 free problems with complete detailed solutions.
Available at the Google Play Store and Apple App Store.