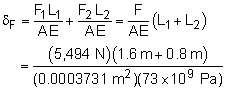| Ch 1. Stress and Strain | Multimedia Engineering Mechanics | ||||||
|
Normal Stress |
Shear and Bearing Stress |
Normal Strain |
Hooke's Law |
Thermal Effects |
Indeterminate Structures |
||
| Indeterminate Axial Structures | Case Intro | Theory | Case Solution | Example |
| Chapter |
| 1. Stress/Strain |
| 2. Torsion |
| 3. Beam Shr/Moment |
| 4. Beam Stresses |
| 5. Beam Deflections |
| 6. Beam-Advanced |
| 7. Stress Analysis |
| 8. Strain Analysis |
| 9. Columns |
| Appendix |
| Basic Math |
| Units |
| Basic Mechanics Eqs |
| Sections |
| Material Properties |
| Structural Shapes |
| Beam Equations |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
|
|
||
|
|
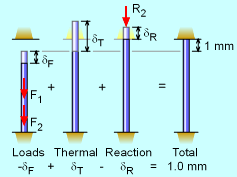
This problem involves both temperature and mechanical loads. Furthermore, the ceiling will restrict the overall deflection of the pole as the temperature increases. The ceiling restriction makes this an indeterminate problem to the first degree (one redundant support or restraint). As such, in addition to the standard equilibrium equations, one compatibility relationship is needed to solve this problem. |
|
| Compatibility Relationship |
||
|
|
When all loads, including thermal, are applied, the structure will have a set deflection, which can be used to define the compatibility condition. Using the concept of superposition, each type of deflection can be isolated. The first deflection, is due to the two shelf loads, F1 and F2, labeled δF. These will compress the pole. Next, the temperature change will cause the pole to increase by δT. This deflection assumes there is no ceiling. But there is a ceiling that will restrict the deflection and cause a compression force and deflection, δR. The total deflection cannot exceed the initial gap of 1 mm. Thus, the compatibility relationship is -δF + δT - δR = 1 mm |
|
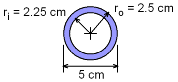 Pipe Cross-Section |
Before finding the pole deflections, the cross-sectional area of the pipe needs to be calculated. A = π (2.52 -
2.252) cm2 |
|
| Deflections |
||
|
|
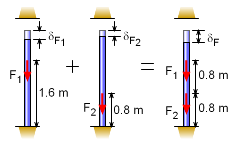
Load Deflection δF = δF1 + δF2 |
|
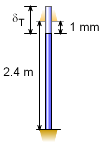 Thermal Deflection without Ceiling |
Thermal Deflection δF =
L α ΔT This total thermal deflection may not be possible due to the ceiling. If it is too great, the ceiling will induce a reaction force into the pole that must be considered. This is calculated in the next paragraph. |
|
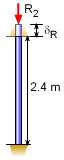 Reaction with Ceiling |
Ceiling Reaction Deflection =
8.8081 × 10-8 R2 m =
0.000088081 R2 mm |
|
| Solving for the Reactions |
||
|
Now that all the deflections have been established, they can be substituted into the compatibility relationship, -δF + δT - δR = 1 mm -0.4842 + 1.6553 - 0.000088081 R2 = 1.0 R2 = 1,943 N |
||
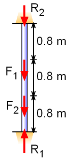 Applied and Reaction Loads |
The reaction is positive, thus the initial assumption that the ceiling will cause compression was correct. The floor reaction can be found by using the static equilibrium equation, ΣFy =
0 R1 = 12.93 kN |
|
Practice Homework and Test problems now available in the 'Eng Mechanics' mobile app
Includes over 500 free problems with complete detailed solutions.
Available at the Google Play Store and Apple App Store.