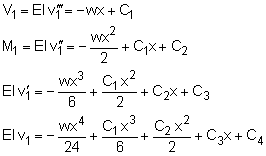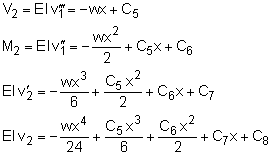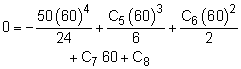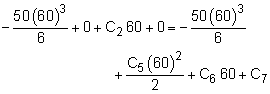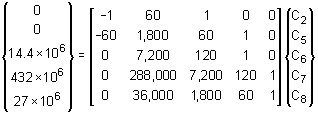| Ch 5. Beam Deflections | Multimedia Engineering Mechanics | ||||||
|
Integration of Moment |
Integration of Load |
Method of Superposition |
Indeterminate Beams |
||||
| Indeterminate Beam Structures | Case Intro | Theory | Case Solution | Example |
| Chapter |
| 1. Stress/Strain |
| 2. Torsion |
| 3. Beam Shr/Moment |
| 4. Beam Stresses |
| 5. Beam Deflections |
| 6. Beam-Advanced |
| 7. Stress Analysis |
| 8. Strain Analysis |
| 9. Columns |
| Appendix |
| Basic Math |
| Units |
| Basic Mechanics Eqs |
| Sections |
| Material Properties |
| Structural Shapes |
| Beam Equations |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
|
|
||||||||||||||||||||
 Beam with Loads |
Example |
|||||||||||||||||||
|
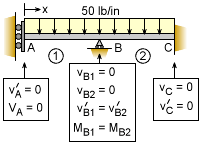
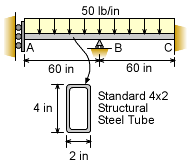
This example is the same problem as the case study previously solved. However, instead of using the principle of superposition, solve for point A deflection by integrating the load-deflection equation. The beam is a standard 4 x 2 structural steel tube. Assume Young 's modulus, E, is 29,000 ksi. |
||||||||||||||||||||
| Solution |
||||||||||||||||||||
|
|
Recall, the load-deflection equation is EIv´´´´ = -w(x) This equation can be integrated four times, but four boundary conditions are required to determine the integration constants. |
|||||||||||||||||||
|
|
The beam in this problem requires two sections due to the center support. This also means that there must be four boundary conditions. These conditions are listed in the diagram at the left. Integrating the load-deflection equation for beam section one gives For the second beam section, integration of the load-deflection equation gives, Now each of the boundary conditions need to be applied which will produce eight equations. They are given below. |
|||||||||||||||||||
|
Boundary Condition 1) Boundary Condition 2) Boundary Condition 3) Boundary Condition 4) Boundary Condition 5) Boundary Condition 6) Boundary Condition 7) Boundary Condition 8) |
|||||||||||||||||||
|
The five equations from boundary conditions 4 through 8 can be used to solve for the 5 unknowns, C2, C5, C6, C7 and C8. These five equations are summarized in matrix form below.
It is difficult to solve these by hand but can easily solved with a matrix solver in most engineering calculators or with a spreadsheet. The solution for the unknowns are C2= 39,000 Using boundary condition 3 gives C4 = -43,200,000 |
||||||||||||||||||||
|
All the integration constants are now known and can be used with the deflection equation. Young's Modulus is 29,000 ksi and the moment of inertia for the 4x2 steel tube is 5.32 in4 (from the Structural Shapes Appendix). EI v1 = -wx4/24 + C1 x3/6 + C2 x2/2 + C3 x + C4 (29,000,000)(5.32) v1 = 0 + 0 + 0 + 0 - 43,200,000 v1 = 0.2800 in This deflection at point A is the same as previously calculated using superposition. |
||||||||||||||||||||
Practice Homework and Test problems now available in the 'Eng Mechanics' mobile app
Includes over 500 free problems with complete detailed solutions.
Available at the Google Play Store and Apple App Store.