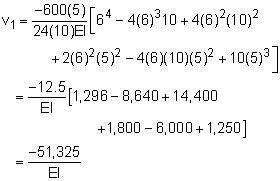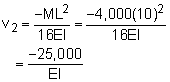| Ch 5. Beam Deflections | Multimedia Engineering Mechanics | ||||||
|
Integration of Moment |
Integration of Load |
Method of Superposition |
Indeterminate Beams |
||||
| Method of Superposition | Case Intro | Theory | Case Solution | Example |
| Chapter |
| 1. Stress/Strain |
| 2. Torsion |
| 3. Beam Shr/Moment |
| 4. Beam Stresses |
| 5. Beam Deflections |
| 6. Beam-Advanced |
| 7. Stress Analysis |
| 8. Strain Analysis |
| 9. Columns |
| Appendix |
| Basic Math |
| Units |
| Basic Mechanics Eqs |
| Sections |
| Material Properties |
| Structural Shapes |
| Beam Equations |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
|
|
||
|
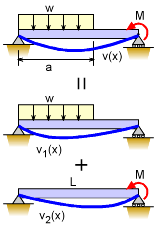
Finding beam deflections using the moment equation or the load-deflection equation can be tedious and lengthy. An alternative method is to use superposition to find the deflection. Basically, a complex beam with its loading is simplified to a series of basic beams (one span) and with only one load. Then the solution to all the simplified beams are added together to give a final solution. |
||
|
|
||
| Superposition for Beam Deflection |
||
|
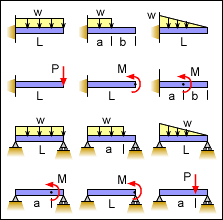
While superposition can be used for many problems in engineering, they are particularly useful for beam deflections. Most beam configuration and loading can be split into simpler beams and loading. For example, the beam at the left with a distributed load and a point moment load can be split into two beams. One with the distributed load and one with the moment load. After the beams are simplified, the deflections of the simplified beams are still needed. To assist engineers, the deflection of simple beams are commonly listed in handbooks. This eBook has many basic beams listed in the Beam Equations appendix. The solutions for these simple beams can be derived by integrating the moment equation or load-deflection equation. The deflection equation of the complex beam is the addition of the two simpler beam equations, or δ(x) = δ1(x) + δ2(x) There are a number of assumptions when using superposition. It is assumed that the beam undergoes linear deflection, all deflections are small, elastic material properties, no shear deflection (i.e. no short thick beams, and normal boundary conditions. |
||
| Superposition Example |
||
|
|
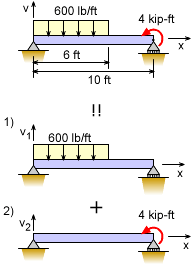
One of the best way to understand the principle of superposition for beam deflection is an example. The same beam as above will be used but with numerical values for the deflection at the beam center. The beam is split into two simpler beams; beam 1) with a distributed load and beam 2) with a point moment load. The deflection for beam 1) with a distributed load over part of the beam is given in the appendix as For the center deflections, x = 5 ft, L = 10 ft, and a = 6 ft, giving, The deflection for beam 2) at the beam's center with a point moment load is given as Summing the two solutions give v = v1 + v2 = -51,325/EI - 25,000/EI = -76,325/EI While this example only has two sub-beam sections, there could be many more, but the process will be the same. |
|
Practice Homework and Test problems now available in the 'Eng Mechanics' mobile app
Includes over 500 free problems with complete detailed solutions.
Available at the Google Play Store and Apple App Store.