| Ch 5. Beam Deflections | Multimedia Engineering Mechanics | ||||||
|
Integration of Moment |
Integration of Load |
Method of Superposition |
Indeterminate Beams |
||||
| Method of Superposition | Case Intro | Theory | Case Solution | Example |
| Chapter |
| 1. Stress/Strain |
| 2. Torsion |
| 3. Beam Shr/Moment |
| 4. Beam Stresses |
| 5. Beam Deflections |
| 6. Beam-Advanced |
| 7. Stress Analysis |
| 8. Strain Analysis |
| 9. Columns |
| Appendix |
| Basic Math |
| Units |
| Basic Equations |
| Sections |
| Material Properties |
| Structural Shapes |
| Beam Equations |
| Search |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| Author(s): |
| Kurt Gramoll |
| ©Kurt Gramoll |
|
|
||
| Example |
||
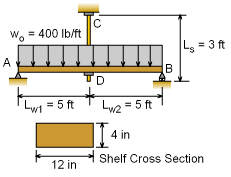 Shelf Supports and Loading |
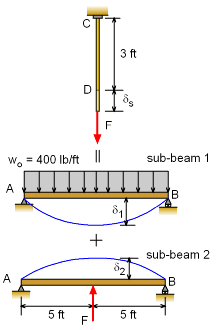
A student has decided to design a book shelf with a center hanger. The wood shelf, AB, is 10 ft in length and has a cross section of 12 in × 4 in (nominal dimension). The wood elasticity modulus, Ew, is 1.5×106 psi. The hanger, CD, is a 3 foot long steel rod with a yield strength of 36 ksi and an elasticity modulus, Es, of 30×106 psi. The hanger just fits between the shelf and ceiling before books are placed on it. The books exert a uniform load of 400 lb/ft on the shelf. Assuming that the beam will not fail due to bending what should be the diameter of the hanger? Use a factor of safety of 3. |
|
| Solution |
||
| The problem can be solved using the method of superposition. This is done by reducing the problem to simpler problems and then adding the solutions together to get the final result. | ||
|
The shelf AB can be considered as a simply supported beam. This beam can be simplified by splitting it into two sub-beams, 1) a simply supported beam with uniform distributed load and 2) a simply supported beam with a point load acting at the center. The point load is actually the unknown force in the rod. Since the rod will also extend due to the load F, the total deflection at point B will be a combination of the two simplified beams and the rod. This can be summarized as δs = δ1 + δ2 The deflections are shown in the diagram on the left. The moment of inertia for the wood beam is Remember, the actual size of a 4x12 wood member is 11.25 in by 3.5 in. These deflections can now be substituted in the deflection compatibility equation to give 1.2×10-6 F/ As = 1.493 - 5.970×10-4 F
|
|
Practice Homework and Test problems now available in the 'Eng Mechanics' mobile app
Includes over 500 free problems with complete detailed solutions.
Available at the Google Play Store and Apple App Store.