| Ch 2. Torsion | Multimedia Engineering Mechanics | ||||||
|
Circular Bars |
Nonuniform & Indeterminate |
Thin-walled Tubes |
Non-Circular Bars | ||||
| Nonuniform & Indeterminate Torsion | Case Intro | Theory | Case Solution | Example |
| Chapter |
| 1. Stress/Strain |
| 2. Torsion |
| 3. Beam Shr/Moment |
| 4. Beam Stresses |
| 5. Beam Deflections |
| 6. Beam-Advanced |
| 7. Stress Analysis |
| 8. Strain Analysis |
| 9. Columns |
| Appendix |
| Basic Math |
| Units |
| Basic Mechanics Eqs |
| Sections |
| Material Properties |
| Structural Shapes |
| Beam Equations |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
|
|
||
| Example |
||
 Example Graphic |
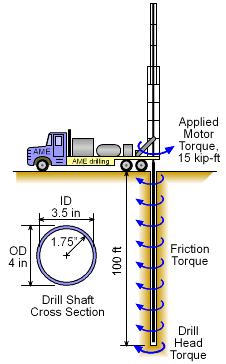
When drilling a hole, the shaft generally has torque resistance at the drill head and also along the length of the shaft. The drill head resistance is caused by the drilling action of cutting away dirt and rock. The shaft torque resistance is due, in part, to the friction of the drilling pipe against the hole surface. If it is assumed that half the torque supplied by the drilling motor is used at the drill head and the other half to overcome the shaft resistance due to friction, what is total angle of twist for the shaft? Assume the shaft resistance is constant along the length of the 100 foot shaft. The drilling pipe is steel with a Young's Modulus, E, of 29,000 ksi and a Poisson's Ratio of 0.29. The pipe outside diameter is 4 inches and inside diameter is 3.5 inches. |
|
| Solution |
||
| In this example, there is a point moment load at the tip of the drill shaft and a constant distributed moment load as shown in the diagram. Thus, the applied moment of 15 kip-ft by the drill motor will be resisted by a constant distributed friction load along the shaft. This friction load is half the applied load and is distributed along the shaft. | ||
|
|
Mfriction = (M/2)x/L = (15 kip-ft/2)
x / 100 ft The drill head has a point moment of half the applied moment or Mdrill head = M/2 = 15 kip-ft / 2 = 7.5 kip-ft The actual internal moment (or torque) is not the same as the applied moment. A simple internal moment diagram can be constructed that shows the change of moment as a function of depth. At the top, there is a 15 kip-ft moment, but is slowly reduced by the friction. At the drill head end of the drill pipe, there remains 7.5 kip-ft internal moment. This moment is used to do the actual drilling. This result can be modeled as function, giving T(x) = 15 - 0.075x kip-ft (where x is in feet) Now that the internal moment function has been determined, the total angle of twist can be calculated using However, the shear modulus, G, and polar moment of inertia, J, are constant and can be moved outside of the integral. Both G and J can be calculated as Also, the moment needs to be converted from kip-ft to kip-in and the integrated length, ft, converted to in. Combining gives, = 1.386 radians or θ = 79.40 degrees |
|
Practice Homework and Test problems now available in the 'Eng Mechanics' mobile app
Includes over 500 free problems with complete detailed solutions.
Available at the Google Play Store and Apple App Store.