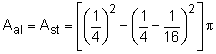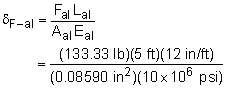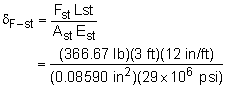| Ch 1. Stress and Strain | Multimedia Engineering Mechanics | ||||||
|
Normal Stress |
Shear and Bearing Stress |
Normal Strain |
Hooke's Law |
Thermal Effects |
Indeterminate Structures |
||
| Thermal Effects | Case Intro | Theory | Case Solution | Example |
| Chapter |
| 1. Stress/Strain |
| 2. Torsion |
| 3. Beam Shr/Moment |
| 4. Beam Stresses |
| 5. Beam Deflections |
| 6. Beam-Advanced |
| 7. Stress Analysis |
| 8. Strain Analysis |
| 9. Columns |
| Appendix |
| Basic Math |
| Units |
| Basic Mechanics Eqs |
| Sections |
| Material Properties |
| Structural Shapes |
| Beam Equations |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
|
|
||
|
|
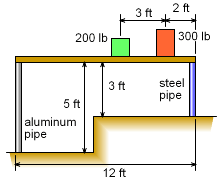
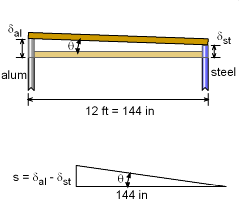
A storage rack is set up over a 2 foot rise in the floor in a warehouse. The rack spans a 12 foot space and is supported by two pipes, one at each end. The left pipe is an aluminum pipe (Eal = 10,000 ksi) and right pipe is a steel pipe (Est = 29,000 ksi). Both pipes have an outside diameter of 1/2" and a wall thickness of 1/16". The rack was constructed in winter at a temperature of 20oF and it was perfectly level. Later in the summer, when the temperature is at 125oF, the two packages are placed on the rack as shown. Thus the change in temperature is 105oF. Since it is critical that the shelf remains nearly level, the angle of rotation of the shelf needs to be calculated. This can be done by determining both the thermal expansion and the compression deflection due to the package loads of both pipes. |
|
| Pipe Thermal Expansion |
||
|
|
Since each pipe is a different length and made of different materials, their overall length changed due to the temperature change will be different. δT-al =
Lal αal (ΔT) δT-st =
Lst αst (ΔT) |
|
| Pipe Compression Load and Deflection |
||
|
|
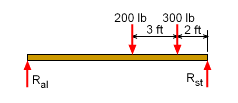
Due to the packages on the rack, there will also be compression loads in the pipes which will shorten the pipes slightly. First, the compression loads in each pipe needs to be determined from basic static equilibrium equations. ΣMst = 0 ΣFy =
0 |
|
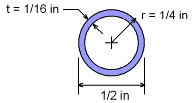 Pipe Cross-Section |
Before finding the deflection, the cross-section area of the pipes needs to be known. |
|
 Pipe Compression Deflection Due to Loads |
Recall, axial deflection is a function of the material length, stiffness, area and load. Now that the load is known, the deflection can be calculated for each pipe as, |
|
| Rack Rotation |
||
|
|
The angle or rotation can now be determined from both the thermal and compression deflections. δal = δT-al - δF-al = 0.8190 - 0.00931 = 0.08097 in δst = δT-st - δF-st = 0.02457 - 0.005299 = 0.01927 in s = δal - δst = 0.08097 in - 0.01927 in = 0.06170 in The angle or rotation, θ, is tanθ = s/144 = 0.06170/144 = 0.0004285 or θ = 0.02455o This is a small angle, so the rack could be considered level. |
|
Practice Homework and Test problems now available in the 'Eng Mechanics' mobile app
Includes over 500 free problems with complete detailed solutions.
Available at the Google Play Store and Apple App Store.