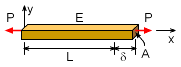| Ch 1. Stress and Strain | Multimedia Engineering Mechanics | ||||||
|
Normal Stress |
Shear and Bearing Stress |
Normal Strain |
Hooke's Law |
Thermal Effects |
Indeterminate Structures |
||
| Normal Strain | Case Intro | Theory | Case Solution | Example |
| Chapter |
| 1. Stress/Strain |
| 2. Torsion |
| 3. Beam Shr/Moment |
| 4. Beam Stresses |
| 5. Beam Deflections |
| 6. Beam-Advanced |
| 7. Stress Analysis |
| 8. Strain Analysis |
| 9. Columns |
| Appendix |
| Basic Math |
| Units |
| Basic Mechanics Eqs |
| Sections |
| Material Properties |
| Structural Shapes |
| Beam Equations |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
|
|
||||||||
| Normal Strain |
||||||||
|
|
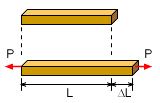
Strain, represented by the Greek letter ε, is a term used to measure the deformation or extension of a body that is subjected to a force or set of forces. The strain of a body is generally defined as the change in length divided by the initial length.
Often, the change in length of the bar, ΔL, is simply referred to as the total displacement, or δ. In that case, strain is then
The elongation of the bar is assumed normal, or perpendicular, to the cross
section. Therefore, like stress, the strain is called a normal strain.
Similar to stress, a tensile strain is generally considered positive and a
compressive strain is considered negative. |
|||||||
| Stress-Strain Relationship |
||||||||
|
|
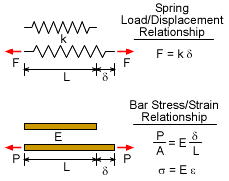
For linearly elastic materials, Hooke's Law relates the stress of a body to the strain in the elastic range. Through experiments, it can be shown that most materials act like springs in that the force is proportional to the displacement (F = kδ). However, unlike a spring, a bar has a cross-sectional area that effects the displacement. Therefore, it is simpler to relate the stress (F/A) to the strain (δ/L). This gives the relationship,
where E is the material property that represents the stiffness of the material (called Young's Modulus). Simply stated, the stress is directly proportional to the strain. Young's modulus is determined through experiments and are commonly listed in engineering handbooks (appendix has a partial list for many common structural materials). This stress-strain relationship is called Hooke's Law. In the next section, this relationship will be expanded to two dimensions. |
|||||||
| Stress-Strain Curve |
||||||||
|
|
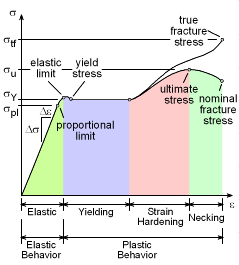
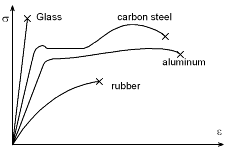
The previous paragraphs developed the basic linear elastic stress-strain relationship assuming there was no plastic deformation. However, if most materials are strained enough, they will permanently deform. When a material deforms, the stress-strain relationship is no longer linear. It is common to plot the stress as a function of the strain. This curve is called the 'Stress-Strain Curve'. Each material has a unique curve, but for most materials, the initial curve is a straight line reflecting the linear relationship between the stress and strain. This is called the 'Elastic' range. Hooke's Law only applies in this range. If the material is stressed past its elastic limit, the material will be permanently deformed and plastic deformation will occur. This means the material has yielded and will stretch easily with little additional load. Next, the material cross-section will become smaller which is called "necking". Since the cross-sectional area is reducing, the effective, or true stress goes up. However, many times the stress calculations will use the original cross sectional area (called the nominal area) and this makes the stress-strain curve appear to go down. While most material have an elastic range, some do not. Rubber has no linear range. Most glasses at room temperature have only an elastic range. Some examples of basic stress-strain curves are given at the left. |
|||||||
| Uniaxial Deflection - Constant Load, Area and Stiffness |
||||||||
|
|
For a simple homogenous bar with a constant cross section and a constant applied load, the total deflection of the bar can be determined in terms of P, L, A, and E. Starting with the one dimensional Hooke's Law, σ = Eε and substituting P/A for stress and δ/L for strain gives, P/A = E (δ/L) This can be rearranged to give,
|
|||||||
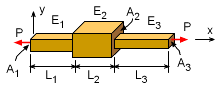 Total Deformation δ = PL1/A1E1 + PL2/A2E2 + PL3/A3E3 |
If there are a series of bars, then the deflection of each section can be determined and then all deflections summed. This can be written in equation form as
|
|||||||
| Uniaxial Deflection - Variable Load, Area and Stiffness |
||||||||
|
|
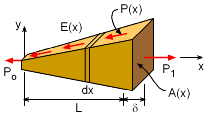
There are cases when the loading, cross section area, and/or the stiffness varies along the bar. In this case, the bar can be split into small infinitesimal lengths, dx, and integrated along its length as
To solve, each of the non-constant parameters (A,E, and P) need to be a function in terms of its length (x in this case). Generally, only one or two of the parameters will be non-constant. An example would be the tapered stake driven into the ground where the area varies and the loading varies due to friction on its surface. |
|||||||
Practice Homework and Test problems now available in the 'Eng Mechanics' mobile app
Includes over 500 free problems with complete detailed solutions.
Available at the Google Play Store and Apple App Store.