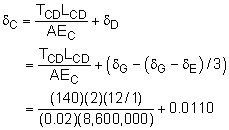| Ch 1. Stress and Strain | Multimedia Engineering Mechanics | ||||||
|
Normal Stress |
Shear and Bearing Stress |
Normal Strain |
Hooke's Law |
Thermal Effects |
Indeterminate Structures |
||
| Normal Strain | Case Intro | Theory | Case Solution | Example |
| Chapter |
| 1. Stress/Strain |
| 2. Torsion |
| 3. Beam Shr/Moment |
| 4. Beam Stresses |
| 5. Beam Deflections |
| 6. Beam-Advanced |
| 7. Stress Analysis |
| 8. Strain Analysis |
| 9. Columns |
| Appendix |
| Basic Math |
| Units |
| Basic Mechanics Eqs |
| Sections |
| Material Properties |
| Structural Shapes |
| Beam Equations |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
|
|
||
|
|
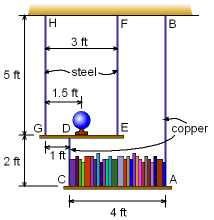
Since the shelves are not symmetrically loaded, each wire will likely have a different load. This will cause each of the wire to deflect differently and thus the shelves to rotate slightly. Complicating the situation is there are two types of wire used, steel and copper, and lengths of the wires vary. |
|
| Load in Wires |
||
|
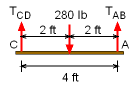
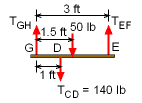
The first step is to determine the load in each wire using static equilibrium equations. Draw a free-body diagram for both shelves so that the load in each wire can be found. Since there are only two known cable forces for the shelf on the bottom shelf, it should be analyzed first. Due to symmetry, it is easy to notice that the tensions in both cables AB and CD will equal half the weight of the books. TAB = TCD = 140 lb Now, the top shelf can be analyzed since the wire load TCD is known which only leaves two unknowns, TGH TEF. The tension in the cable EF can be calculated by summing the moments about point G, ΣMG = 3TEF - 1.5 (50) - 1 (140) = 0 TEF = 71.67 lb Summing forces in the vertical direction gives the force in cable GH, ΣFy = TGH - 140 - 50 + TEF = 0 TGH = 118.3 lb |
||
| Wire Elongation and Shelf Rotation |
||
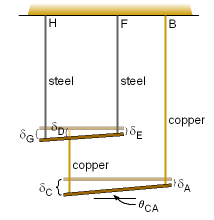 Shelf Deflection and Rotation |
The tensions in the cables will cause each wire to stretch a small amount. The elongation of each wire can be found from the equation where P is the force, L is the length, A is the cross-sectional area, and E is the Young's modulus of each wire. The elongation of each cable will cause each of the points A, C, D, E, and G to be displaced differently, as shown. The angle of rotation of the bottom shelf is given by Therefore, the deflection of points A and C need to be calculated. The deflection at point A is simply the elongation of the wire AB, |
|
|
|
The deflection at point C is more complex to determine since it is related to the deflection of the top shelf. However, the total deflection is simply the sum of the elongation of CD and the deflection of point D, The displacement at point D is related to the displacement at points E and G as δD = δG - (δG - δE)/3 However, this requires the deflection of points E and G to be determined. The deflection at point E is equal to the elongation of the wire EF, The deflection at point G is Substituting these results back into the the δC deflection equation gives, |
|
|
Now the rotation angle can be determined, = 0.04513o The negative sign inside the arctan term simply means the angle is opposite of the assumed direction in the diagram above. |
||
Practice Homework and Test problems now available in the 'Eng Mechanics' mobile app
Includes over 500 free problems with complete detailed solutions.
Available at the Google Play Store and Apple App Store.