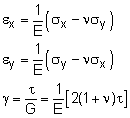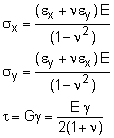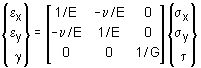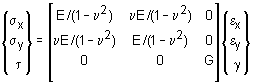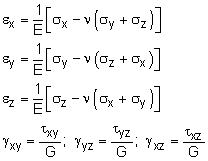| Ch 1. Stress and Strain | Multimedia Engineering Mechanics | ||||||
|
Normal Stress |
Shear and Bearing Stress |
Normal Strain |
Hooke's Law |
Thermal Effects |
Indeterminate Structures |
||
| Hooke's Law | Case Intro | Theory | Case Solution | Example |
| Chapter |
| 1. Stress/Strain |
| 2. Torsion |
| 3. Beam Shr/Moment |
| 4. Beam Stresses |
| 5. Beam Deflections |
| 6. Beam-Advanced |
| 7. Stress Analysis |
| 8. Strain Analysis |
| 9. Columns |
| Appendix |
| Basic Math |
| Units |
| Basic Mechanics Eqs |
| Sections |
| Material Properties |
| Structural Shapes |
| Beam Equations |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
|
|
||||||||||||||
| One Dimensional Hooke's Law |
||||||||||||||
|
|
Recall, Hooke's Law in one dimension (uniaxial loading), relates the normal stress and normal strain as
The constant E is Young's modulus and represents the stiffness of the the material. |
|||||||||||||
| Poisson's Ratio |
||||||||||||||
|
|
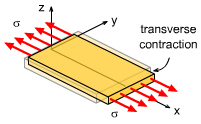
When analyzing more than one dimension, interaction between all directions needs to be considered. This is done through Poisson's ratio. Basically, Poisson's ratio is the amount of transverse contraction, or negative strain, when strained in a given direction. For a basic object pulled or strained in the x-direction, the Poisson's Ratio is defined as
Thus, when a member is pulled in the x-direction, there is a contraction strain in the y-direction (and z-direction). If it is pulled in the y-direction, then the contraction strain will be in the x-direction (and z-direction). For a three dimensional object, Poisson's ratio will occur in equally in both perpendicular directions. If the load is in the x-direction, then strain in the y- and z-direction will be εy = εz = -νεx |
|||||||||||||
| Two Dimensional Stress-Strain |
||||||||||||||
|
|
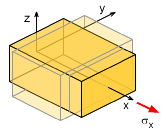
If a material is isotropic (homogenous in all directions, such as a solid metal) and is pulled in two directions, then due to Poisson's ratio, the overall normal strain will be the total of the two strains. For example, if there are normal stresses in both the x- and y-directions, then the total normal strain in the x-direction is εx total = εx due to σx + εx due to σy = σx /E - νσy/E εx = (σx - νσy) / E Similarly, the normal strain in the y-direction would be εy = (σy - νσx) / E |
|||||||||||||
|
|
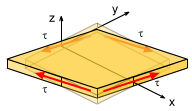
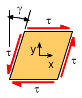
However, Hooke's Law also relates shear strain and shear stress. If the shear stress and strain occurs in a plane then the stress and strain are related as
or γ = τ/G = [2(1 + ν)/E] τ where G is the shear modulus (a material property) and γ is the shear strain. The shear strain is defined as the angle (radians) caused by the shear stress as shown in the diagram at the left. The shear modulus is related to Young modulus and Poisson's ratio,
Two dimensional stress-strain relationships are summarized in the table below. |
|||||||||||||
|
||||||||||||||
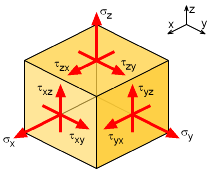
| Three Dimensional Stress-Strain |
||||||||||||||
|
|
Just like 1D or 2D, Hooke's Law can also be applied to material undergoing three dimensional stress (triaxial loading). The development of 3D equations is similar to 2D, sum the total normal strain in one direction due to loads in all three directions. For the x-direction, this gives, εx total = εx due to σx + εx due to σy + εx due to σz = σx /E - νσy/E - νσz/E εx = (σx - νσy - νσy) / E Similarly, the other directions can also be determined. The final equations are summarized in the table below. |
|||||||||||||
|
||||||||||||||
| 3D Elasticity |
||||||||||||||
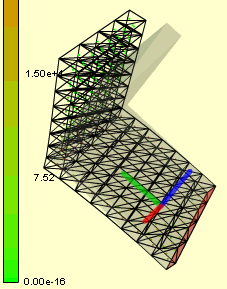
In addition to the Hooke's Law, complex stresses can be determined using the theory of elasticity. This topic is beyond this text, but through the use of compatibility and equilibrium equations, complex 3D stresses can be determined by numerical methods. The numerical method most commonly used is finite element analysis (FEA) and is widely used in industry. Just a few of the many commercial FEA codes include ANSYS, Cosmos, NISA, Abaqus, and AutoDesk, SolidWorks, many more. |
||||||||||||||
Practice Homework and Test problems now available in the 'Eng Mechanics' mobile app
Includes over 500 free problems with complete detailed solutions.
Available at the Google Play Store and Apple App Store.