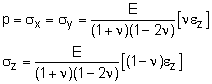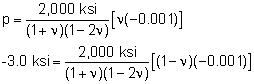| Ch 1. Stress and Strain | Multimedia Engineering Mechanics | ||||||
|
Normal Stress |
Shear and Bearing Stress |
Normal Strain |
Hooke's Law |
Thermal Effects |
Indeterminate Structures |
||
| Hooke's Law | Case Intro | Theory | Case Solution | Example |
| Chapter |
| 1. Stress/Strain |
| 2. Torsion |
| 3. Beam Shr/Moment |
| 4. Beam Stresses |
| 5. Beam Deflections |
| 6. Beam-Advanced |
| 7. Stress Analysis |
| 8. Strain Analysis |
| 9. Columns |
| Appendix |
| Basic Math |
| Units |
| Basic Mechanics Eqs |
| Sections |
| Material Properties |
| Structural Shapes |
| Beam Equations |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
|
|
||
|
|
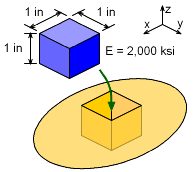
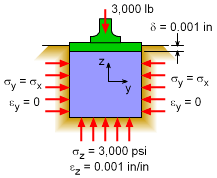
A simple cube of material is inserted into a snug fitting test frame and then a 3,000 lb load is applied on the top surface. The sides of the test frame are stiff and will not deflect at the test load level. Also, the sides are smooth so there is no friction forces as the specimen is loaded. The objective in testing the specimen is to determine the Poisson's ratio of the material. The Young's modulus, E, is known, 2,000 ksi. Also, the total deflection after loading is 0.001 inches. |
|
| Determining Poisson's ratio |
||
|
|
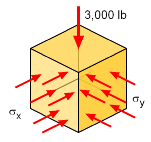
A good place to start solving this problem is the full 3D Hooke's law equations. While these look complex, many terms are easily determined. The vertical stress can be calculated as σz = F/A = 3000 lb/(1 in)2 = 3,000 psi = 3.0 ksi The other two horizontal stresses are unknown, but must be the same due to symmetric geometry and loading. Thus, σx = σy = p |
|
 Problem Diagram |
Next, the three strains can be determined. The vertical strain can be found since the deflection is known, giving εz = δ/L = (0.001 in) / (1.0 in) = 0.001 The other two strains are also known since the outside walls do not deflect (due to their high stiffness). Thus, εx = εy = 0.0 Also, Young's modulus is known, E = 2,000 ksi. |
|
 Graph of Function f(ν) = (1-ν) / [(1+ν)(1-2ν)] |
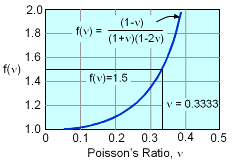
Simplifying the 3D equations to two equations give, Next, substituting specific values reduce these equations to The negative signs represent compression for both strain and stress. There are now two unknowns, p and ν. The second equation can be rearranged to give, This can be manipulated to give 3ν2 + 0.5ν - 0.5 = 0 Using the quadratic equation, the positive root gives ν = 0.3333 This equation can also be solved numerically by graphical methods or by using numerical programs like MathCad, Mathematica, MathLab, or even Excel. The equation is graphed at the left which also gives ν = 0.3333 |
|
| Stresses |
||
|
|
The stresses in the x and y directions can now be determined, p = σx = σy = -1.5 ksi = 1,500 psi |
|
Practice Homework and Test problems now available in the 'Eng Mechanics' mobile app
Includes over 500 free problems with complete detailed solutions.
Available at the Google Play Store and Apple App Store.