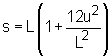| Ch 3. Derivatives II | Multimedia Engineering Math | ||||||
|
Higher Order Derivatives |
Related Rates |
Differential |
Newton's Method |
||||
| Differential | Case Intro | Theory | Case Solution |
| Chapter |
| 1. Limits |
| 2. Derivatives I |
| 3. Derivatives II |
| 4. Mean Value |
| 5. Curve Sketching |
| 6. Integrals |
| 7. Inverse Functions |
| 8. Integration Tech. |
| 9. Integrate App. |
| 10. Parametric Eqs. |
| 11. Polar Coord. |
| 12. Series |
| Appendix |
| Basic Math |
| Units |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
| |
||
| Introduction |
||
|
|
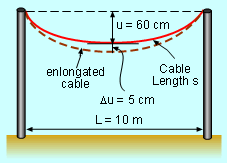
An electric cable company is replacing the old cable in Dallas. Without the supporting steel cable, the electric cable that hangs between two poles form an arc because of the gravity. In the summer, the cable sinks for about 5 cm due to temperature, how much does the cable elongate? What is known:
|
|
| Questions |
||
| How much does the cable elongate when its lowest point goes down for 5 cm? |
||
| Approach |
||
|
||