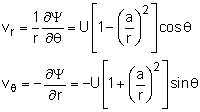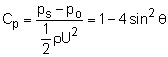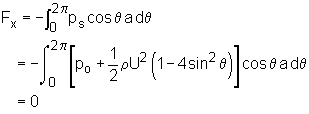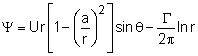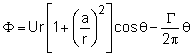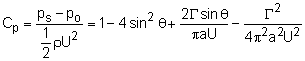| Ch 7. Incompressible and Inviscid Flow | Multimedia Engineering Fluids | ||||||
|
Bernoulli's Equation |
Flow Measurements |
Superposition of Flows |
Flow around Cylinder |
||||
| Flow around a Circular Cylinder | Case Intro | Theory | Case Solution |
| Chapter |
| 1. Basics |
| 2. Fluid Statics |
| 3. Kinematics |
| 4. Laws (Integral) |
| 5. Laws (Diff.) |
| 6. Modeling/Similitude |
| 7. Inviscid |
| 8. Viscous |
| 9. External Flow |
| 10. Open-Channel |
| Appendix |
| Basic Math |
| Units |
| Basic Fluid Eqs |
| Water/Air Tables |
| Sections |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
|
|
||
|
In this section, the solutions for potential flow past a fixed and rotating circular cylinder will be obtained by the method of superposition. |
||
| Flow Past a Fixed Circular Cylinder |
||
|
|
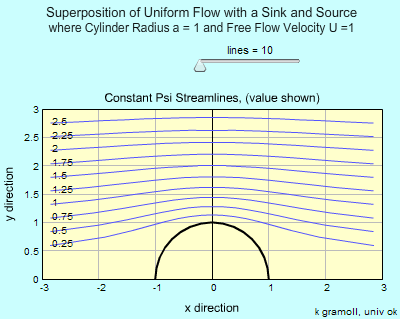
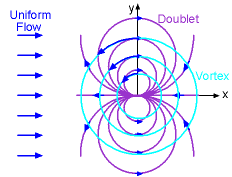
Flow past a fixed circular cylinder can be obtained by combining uniform flow with a doublet. The superimposed stream function and velocity potential are given by Ψ = Ψuniform flow + Ψdoublet = U r sinθ - K sinθ/r and Φ = Φuniform
flow + Φdoublet = U r cosθ +
K cosθ/r Ψ = U a sinθ - K sinθ/a = 0 which gives the strength of the doublet as K = U a2 The stream function and velocity potential for flow past a fixed circular cylinder become Ψ = Ur [1 - (a/r)2] sinθ and Φ = Ur [1 + (a/r)2] cosθ |
|
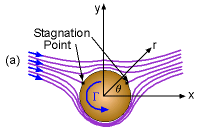
respectively. The plot of the streamlines is shown in the figure. The velocity components can be determined by: Along the cylinder (r = a), the velocity components reduce to vr = 0 and vθ = -2U sinθ The radial velocity component is always zero along the cylinder while the tangential velocity component varies from 0 at the stagnation point (θ = π) to a maximum velocity of 2U at the top and bottom of the cylinder (θ = π/2 or -π/2). The pressure distribution along the cylinder can be obtained using Bernoulli's equation, |
||
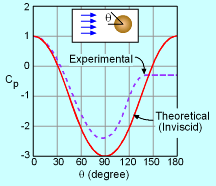 Comparison between Experimental and Theoretical Potential Flow Results |
where the subscript "o" refers to the upstream condition while the subscript "s" refers to the condition along the cylinder. The elevation changes are assumed negligible. Substituting the expression for vθs into the above equation and rearranging gives where Cp is the dimensionless pressure coefficient. The plot of Cp as a function of θ is shown in the figure. The discrepancy between the experimental and theoretical results, as shown in the figure, is due to the viscous effects. |
|
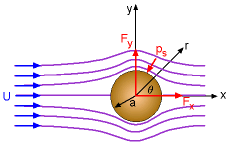 Drag and Lift |
The concepts of drag and lift will be briefly introduced here. The drag developed on the cylinder can be obtained by integrating the pressure over the cylinder surface as, Drag is the resultant force exerted by the fluid on the cylinder, and its direction is parallel to the upstream uniform flow direction. The lift is the resultant force acting perpendicular to the uniform flow direction, and it can be obtained by When the integrations are carried out for Fx and Fy (integration details are not given for simplicity), it is found that both drag and lift are zero for potential flow. The potential flow solutions developed in this section are based on the assumption of inviscid flow (i.e., zero viscosity), which implies that drag vanishes. However, as will be discussed in the Lift section, when a real fluid flows past a cylinder, viscous effects are important near the cylinder. Viscous effects will cause the flow to separate away from the cylinder, and the drag is nonzero in actual flow situations. This discrepancy is referred to as d'Alembert's paradox. |
|
|
||
| Flow Past a Rotating Circular Cylinder |
||
|
Superposition of a Uniform Flow,
|
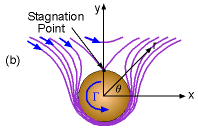
When the solutions obtained previously for flow past a fixed cylinder are combined with a vortex, flow past a rotating cylinder can be simulated. The superimposed stream function and velocity potential now consist of three components and are given by where Γ is the strength of the vortex circulation. The radial velocity vr is still zero along the cylinder surface while the tangential velocity is given by, From the above equation, it can be found that the location of the stagnation point, θstag, depends on the strength of the circulation. Setting vθ equal to zero and yields The streamlines along with the location of the stagnation point for different dimensionless circulation strengths ( Γ / [2πaU] ) are shown in the figure. The pressure distribution along the cylinder surface can be obtained by Bernoulli's equation, giving This is generally rearranged in terms of the dimensionless pressure coefficient, Cp, The drag and lift are obtained by integrating the pressure over the cylinder surface, giving Fx = 0 and Fy = -ρUΓ Hence, there is still no drag for a rotating cylinder (inviscid assumption). However, there is lift involved, and it is directly proportional to the density, upstream velocity and strength of the vortex (Kutta-Joukowski law). The lifting effect for rotating bodies in a free stream is called the Magnus effect. |
|
Practice Homework and Test problems now available in the 'Eng Fluids' mobile app
Includes over 250 free problems with complete detailed solutions.
Available at the Google Play Store and Apple App Store.