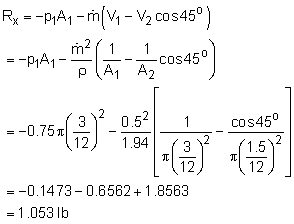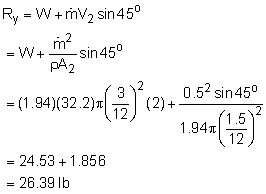Problem Description

Forces on the Control Volume

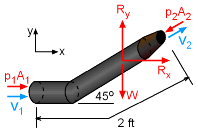
First select a control volume to include the hose, nozzle and water inside the hose, as shown by the red dashed lines in the figure. R_x and R_y represent the reaction force components acting on the hose. W is the weight of the water inside the hose.

The linear momentum equation for steady flow is given by

which can be written in terms of x- and y- component as follows:

    x-component:
    p₁A₁ - p₂A₂cos45^o + R_x
                      = V₁ρ(-V₁)A₁ + V₂cos45^oρ(V₂)A₂

    y-component:
    - p₂A₂sin45^o - W + R_y = V₂sin45^oρ(V₂)A₂

The gage pressure at the nozzle outlet is zero (i.e., p₂ = 0) since water is discharged to the atmosphere. According to the principle of conservation of mass,

The linear momentum equations can be simplified to yield the reaction force in the x- direction:

    

Required Resultant Force for
Holding the Hose in Place

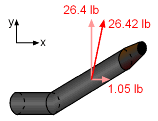
and the reaction force in the y-direction:

     

Hence, the resultant force required to hold the hose in place is given by F = 1.05i + 26.4j lb.