| Ch 4. Fundamental Laws (Integral Anal.) | Multimedia Engineering Fluids | ||||||
|
Conservation Mass |
Linear Momentum |
Moment of Momentum |
Conservation Energy |
||||
| Linear Momentum Equation | Case Intro | Theory | Case Solution |
| Chapter |
| 1. Basics |
| 2. Fluid Statics |
| 3. Kinematics |
| 4. Laws (Integral) |
| 5. Laws (Diff.) |
| 6. Modeling/Similitude |
| 7. Inviscid |
| 8. Viscous |
| 9. External Flow |
| 10. Open-Channel |
| Appendix |
| Basic Math |
| Units |
| Basic Fluid Eqs |
| Water/Air Tables |
| Sections |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
|
|
|||||
|
The linear momentum equation will be presented in this section. The details of the derivation are omitted, with attention focused on proper use of the equation. |
|||||
| Linear Momentum Equation |
|||||
|
|
Linear momentum equation for fluids can be developed using Newton's 2nd Law which states that sum of all forces must equal the time rate of change of the momentum, ΣF = d(mV)/dt. This easy to apply in particle mechanics, but for fluids, it gets more complex due to the control volume (and not individual particles). The change of momentum will have two parts, momentum inside the control volume, and momentum passing through the surface. This concept can be written as |
||||
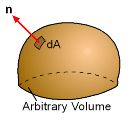 Unit Normal Vector Click to view movie (22k) |
where V is the velocity vector, n is the outward unit normal vector, and ΣF represents the sum of all forces (body and surface forces) applied to the control volume. The actual derivation of this equation is omitted but can be easily done using Reynolds Transport Theorem. This is similar to the conservation of mass equation, but it has an added velocity term in each integral. Also, the sum is not zero, but equal to all the applied forces. Physically, the linear momentum equation states that the sum of all forces applied on the control volume is equal to the sum of the rate of change of momentum inside the control volume and the net flux of momentum through the control surface. For steady flow, the first term on the right hand side vanishes. The sign of the force and velocity vectors (F and V) depends on the assigned coordinate system. The sign on the quantity V·n depends on the velocity as well as the orientation of the control surface. The unit normal vector is defined as positive when pointing out of the control surface. |
||||
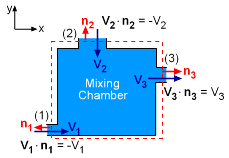 Mixing Chamber Click to view movie (37k) |
To better understand normal directions and signs, consider the mixing chamber as shown in the diagram at the left. At the inlet 1, the flow is in the positive x-direction (i.e., V1 = V1i), while the unit normal is defined out of the control surface n1 = -i. Hence, the term V1·n1 yields a negative value (-V1). The flow at the inlet 2 is in the negative y-direction (i.e.,V2 = -V2j), while the unit normal vector n2 is in the positive y-direction. The term V2·n2 also yields a negative value (-V2). At outlet 3, both the velocity and unit normal vector are in the positive x-direction, hence V3·n3 is positive (V3). The vector form of the linear momentum equation can be written in scalar form once a coordinate system is established. For example, the vector equation can be rewritten in terms of x-, y- and z-components for a Cartesian coordinate system. |
||||
| Steady State Condition |
|||||
As a special case, the conservation of momentum can be simplified for steady state conditions. Assuming simple inlets and outlets from the control volume, i.e. flat and uniform flow, the momentum equation becomes Using the continuity condition, dm/dt = ρAV, the momentum equation simplifies to ΣF = Σ dmi/dt Vi where i represents each outlet and inlet (sign difference). This form of the momentum equation is useful when the mass flow rate is involved, just as water jets or rocket exhaust. |
|||||
| An Example: Pipe Elbow |
|||||
|
To further illustrate the use of the linear momentum equation, consider a pipe elbow as shown in the figure on the right with steady fluid flowing from one end to the other. Also assume a pressure, p, at each end (can be different). Now apply the linear momentum equation to find the reaction forces (Rx, Ry and Rz) applied on the selected control volume. For steady flow there is no change in momentum inside the pipe (control volume) and the linear momentum equation reduces to Next, the inlet and outlet are flat surfaces, and it can be assumed the velocity is uniform across the surface. This reduces the equation to (rewritten in terms of x-, y- and z-components), |
||||
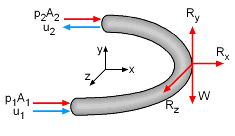 Forces on the Control Volume |
x: p1A1 +
p2A2 + Rx = u1ρ(-u1)A1 -
u2ρ(u2)A2
where W is the weight of the pipe elbow including water. According to the principle of conservation of mass, |
||||
Practice Homework and Test problems now available in the 'Eng Fluids' mobile app
Includes over 250 free problems with complete detailed solutions.
Available at the Google Play Store and Apple App Store.
