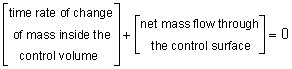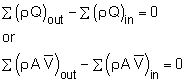| Ch 4. Fundamental Laws (Integral Anal.) | Multimedia Engineering Fluids | ||||||
|
Conservation Mass |
Linear Momentum |
Moment of Momentum |
Conservation Energy |
||||
| Conservation of Mass | Case Intro | Theory | Case Solution | Example |
| Chapter |
| 1. Basics |
| 2. Fluid Statics |
| 3. Kinematics |
| 4. Laws (Integral) |
| 5. Laws (Diff.) |
| 6. Modeling/Similitude |
| 7. Inviscid |
| 8. Viscous |
| 9. External Flow |
| 10. Open-Channel |
| Appendix |
| Basic Math |
| Units |
| Basic Fluid Eqs |
| Water/Air Tables |
| Sections |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
| |
|||||
| In this section, the definitions of a system and control volume are stated. The principle of conservation of mass will be introduced. The conservation of mass equation in integral form will be presented for both fixed and moving control volumes. |
|||||
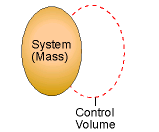
| Definitions: System and Control Volume |
|||||
| A system is a fixed quantity of matter, and no mass is allowed to cross the system boundary. A control volume is a space of interest where mass can cross the boundary. The boundary of the control volume is called the control surface. |
|||||
| Conservation of Mass Equation: Fixed, Nondeforming Control Volume |
|||||
|
|
As the name implies, the principle of conservation of mass states that mass is conserved for a system. Applying the conservation of mass principle for a fixed and nondeforming control volume: The statement above can be easily expressed in mathematical form to yield the conservation of mass equation for a control volume as where n is the outward unit normal vector, which is used to describe the orientation of the control surface. Hence the net mass flow out of the control volume is considered positive. For steady flows, the total mass in the control volume will not vary with time, and the first term vanishes. The second term in the conservation of mass equation represents the net mass flow through the control surface. For control volume with a finite number of faces, it is sometimes convenient to write it in discrete form as |
||||
where
where ρ is the density of the fluid, Q is the volumetric flow rate and If there is just one inlet and one outlet and the density does not change, which is common, this relationship is simply, A1V1 = A2V2 |
|||||
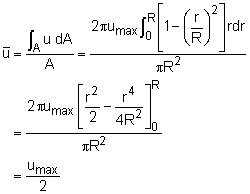
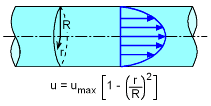 Pipe Flow with Parabolic Velocity Profile |
The average velocity can be obtained by Consider flow in a pipe as shown in the figure. The average velocity can be obtained by integrating the parabolic velocity profile to yield |
||||
| Conservation of Mass Equation: Moving, Nondeforming Control Volume |
|||||
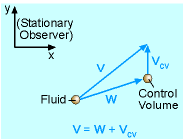
Relative Velocity |
The conservation of mass equation for a moving and nondeforming control volume is the same as described above, but the velocity V is replaced with the relative velocity W. From a stationary observer point of view, the control volume moves at a velocity Vcv, while the fluid moves at a velocity of V. W is the relative velocity of the fluid with respect to the moving control volume. These velocities are related by V = W + Vcv |
||||
Practice Homework and Test problems now available in the 'Eng Fluids' mobile app
Includes over 250 free problems with complete detailed solutions.
Available at the Google Play Store and Apple App Store.