FLUID MECHANICS - THEORY
|
| |
|
The concept of absolute and gage pressure
is discussed in this section. Several common pressure measurement
devices and techniques are also introduced.
|
|
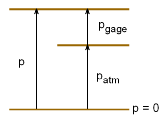
Gage Pressure
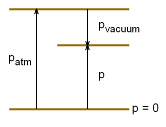
Vacuum
Pressure
|
|
|
| |
Absolute and Gage Pressure
|
| |
When pressure is measured relative to absolute zero pressure, it is called absolute pressure. On the other hand, pressure measuring devices often use gage pressure, which is measured relative to atmospheric pressure. Standard atmospheric pressure at sea level is 101.3 kPa or 14.7 psi. Gage pressure is referred to as vacuum or suction pressure when it is negative.
Gage Pressure: pgage
= pabsolute - patm
Vacuum Pressure: pvacuum = patm - pabsolute
For example, when the driver's manual for your car suggests that you
keep your tires at a pressure of 30 psi, it is refering to the gage pressure. This is equivalent to 44.7 psi absolute pressure.
|
| |
|
|
| |
|
Barometer
|
|
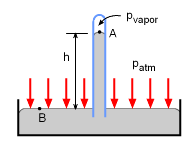
Mercury Barometer
|
|
Atmospheric pressure can be measured through
a mercury barometer. A simple barometer consists of an inverted glass
tube filled with mercury with its open end submerged in a mercury container.
According to the hydrostatic pressure distribution derived
in the last section, the atmospheric pressure is given by
patm = ρgh
+ pvapor
The vapor pressure in the glass tube is negligibly small, hence the atmospheric
pressure is simply given by the height of the mercury column:
patm = ρgh
For example, a column height of 760 mm Hg corresponds to the standard
atmospheric pressure of 101.3 kPa (14.7 psi) at sea level. If water is substituted
for mercury, then a column height of 10.3 m H2O is needed
for atmospheric pressure.
|
| |
|
Piezometer
|

Piezometer
|
|
A piezometer is the simplest form of a pressure
measuring device. It has a vertical tube connected to the container in
which the
pressure is needed. The pressure head of the fluid column indicates the
pressure of the container:
pA = ρgh
where pA is the gage pressure at point A within the container.
The disadvantages of piezometers are:
(1) Cannot measure vacuum pressure since air would be sucked into
the container through the tube.
(2) The measured pressure should be reasonably low, otherwise a very
long vertical tube is needed.
|
| |
|
|
| |
|
Manometer
|
|
|
Another pressure measuring device is the manometer.
It consists of a U-tube with one end connected to the container with
an unknown pressure and the other end open to the
known atmospheric pressure. The fluid in the U-tube manometer (gage
fluid) can be different from the fluid in the container.
The procedure for determining the pressure inside the container is:
(1) Start from one end, and work from one fluid level to another,
up to the open end of the manometer.
(2) Remember that pressure increases linearly with depth for a fluid at
rest. |
| |
|
|

U-Tube Manometer
|
|
Consider the U-tube manometer shown. The pressure at point A inside
the tank is calculated as:
pA + ρ1gh1 - ρ2gh2 = 0
which gives:
pA = ρ2gh2 - ρ1gh1
Once again, gage pressure is used in the above equation (i.e., theatmospheric pressure at the open end is zero gage). If the fluid in the tank is a gas, then the pressure between point 1 and 2 is negligible, hence
pA = ρ2gh2 |
| |
|
|
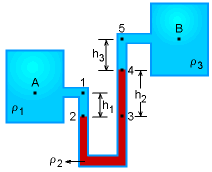
Differential U-Tube Manometer |
|
The U-tube manometer also can be used to determine the pressure difference
between two systems. This type of manometer is called a differential
U-tube manometer. Consider the differential manometer connected between tanks
A and B, as shown in the figure. The pressure will be determined by moving from point A to point B:
pA + ρ1gh1 - ρ2gh2 - ρ3gh3 = pB
The pressure difference is given by
pA - pB = ρ2gh2 + ρ3gh3 - ρ1gh1 |
| |
|
|
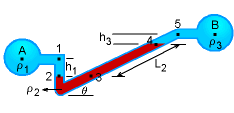
Inclined-Tube Manometer |
|
Another type of manometer is the inclined-tube manometer which is used
to measure small pressure differences between two systems (say for gases).
The advantage of the inclined manometer is that the differential reading scales along the
tube can be made large compared to a vertical manometer for a given
pressure difference, hence improving the accuracy in reading the scale.
The pressure difference between point A and B is given by
pA + ρ1gh1 - ρ2gL2sinθ - ρ3gh3 = pB
For cases where the columns h1 and h3 are gas, the weights can be neglected, simplifying the equation
pA - pB = ρ2gL2 sinθ |
| |
|
|






