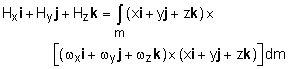| Ch 9. 3-D Motion of a Rigid Body | Multimedia Engineering Dynamics | ||||||
| Translating Coordinates | Rotating Coordinates | Inertia & Ang. Momentum |
Equations of Motion |
||||
| Inertial Prop./Angular Momentum | Case Intro | Theory | Case Solution |
| Chapter |
| - Particle - |
| 1. General Motion |
| 2. Force & Accel. |
| 3. Energy |
| 4. Momentum |
| - Rigid Body - |
| 5. General Motion |
| 6. Force & Accel. |
| 7. Energy |
| 8. Momentum |
| 9. 3-D Motion |
| 10. Vibrations |
| Appendix |
| Basic Math |
| Units |
| Basic Dynamics Eqs |
| Sections |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
|
|
|||||||||||
|
Chapter 6 introduced moment of inertia to describe the angular motion of a rigid body in a plane. To analyze motion in 3-D, moments of inertia is still used but an additional term, product of inertia, must also be determined. |
|||||||||||
| Moment of Inertia |
|||||||||||
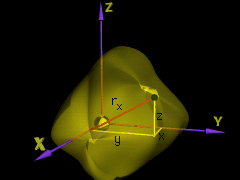 Coordinate System |
Recall, the moment of inertia of the element dm about the x axis is defined as dIxx = rx2 dm (noting rx2 = y2 + z2) Integrating over the mass, gives, Thus, all three directions are |
||||||||||
| Product of Inertia |
|||||||||||
|
The product of inertia of the element dm is defined in relation to a set of two orthogonal planes as the product of the mass of the element and the perpendicular distance from the planes to the element. For example, the product of inertia of an element with respect to the x-z and y-z planes is dIxy = xy dm Integrating over the mass, gives, For all three directions are |
|||||||||||
| Parallel Axis and Parallel Plane Theorems |
|||||||||||
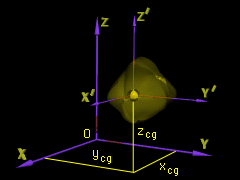 Center of Gravity Dimensions |
If the center of gravity of the body is located at xcg, ycg, zcg within the xyz system, the parallel axis equations are
Using a similar analysis, the parallel plane equations can be derived that transfer the products of inertia from a set of orthogonal planes passing through the body's center of gravity to a parallel set of planes passing through some other point O,
|
||||||||||
| Angular Momentum |
|||||||||||
|
|
Consider a rigid body moving in general motion relative to an inertial reference frame XYZ. The origin A of the xyz axes translates and rotates with the rigid body, which has an angular velocity ω relative to XYZ. Now find the angular momentum of the body about point A relative to XYZ. The angular momentum of the ith particle, with mass mi, about point A is HA-i = ρi/A × mivi where ρi/A represents the position vector from A to the mass element, mi. For simplicity, it will be noted as ρi. Recall, the velocity vi is given by vi = vA + ω × ρi |
||||||||||
Substituting and integrating over the mass, gives If A is located at the center of gravity, the first term in H is zero. This gives, If A is a fixed point O about which the mass rotates, vA = 0, then it is similar to the cg form, If A is an arbitrary point on the body, the total angular momentum reduces to |
|||||||||||
Note that Eqs. 5, 6, and 7 all contain the general form If the coordinate system is rectangular (xyz), then the three components are, Expanding the cross products, combining terms, and making use of Eqs. 1, the angular momentum for xyz coordinate system is
These represent the scalar forms of Eqs. 5 or 6. |
|||||||||||
Practice Homework and Test problems now available in the 'Eng Dynamics' mobile app
Includes over 400 free problems with complete detailed solutions.
Available at the Google Play Store and Apple App Store.