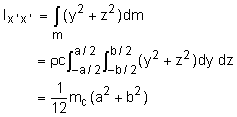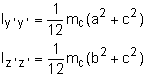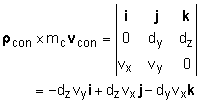| Ch 9. 3-D Motion of a Rigid Body | Multimedia Engineering Dynamics | ||||||
| Translating Coordinates | Rotating Coordinates | Inertia & Ang. Momentum |
Equations of Motion |
||||
| Inertial Prop./Angular Momentum | Case Intro | Theory | Case Solution |
| Chapter |
| - Particle - |
| 1. General Motion |
| 2. Force & Accel. |
| 3. Energy |
| 4. Momentum |
| - Rigid Body - |
| 5. General Motion |
| 6. Force & Accel. |
| 7. Energy |
| 8. Momentum |
| 9. 3-D Motion |
| 10. Vibrations |
| Appendix |
| Basic Math |
| Units |
| Basic Dynamics Eqs |
| Sections |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
|
|
||
| Solution of a) |
||
|
Begin with a diagram, modeling the hull as a circular cylinder and the con as a rectangular prism. Use Eqs. 1 to determine the moments of inertia of the con about its center of gravity: (Note, dm = ρ c dy dz) Using a similar derivation, we get These expressions for the moment of inertia could also be found from Appendix B, or a table of inertial properties. Equations 2 give the products of inertia of the con about its center of gravity: (Note, dm = ρ a dx dy) Using a similar derivation, we get Iy'z' = Ix'z' = 0 |
||
|
|
The expressions for the products of inertia could have been determined simply by noting that the product of inertia about a plane of symmetry is always zero. Use the parallel axis theorem (Eqs. 3) to transfer the moment of inertia of the con about its center of gravity to the center of gravity of the sub: Ixx = Ix'x' + mc (dy2 + dz2) Iyy = 1/12 mc(a2 + c2) + mc (dx2 + dz2) Izz = 1/12 mc(b2 + c2) + mc (dx2 + dy2) Use the parallel plane theorem (Eqs. 4) to transfer the product of inertia of the con about its center of gravity to the center of gravity of the sub: Ixy = Ix'y' + mrdxdy Iyz = mcdydz Ixz = 0 |
|
| Solution of b) |
||
|
Use Eq. 8 to express the angular momentum of the con about its center of gravity (Eq. 5) in scalar form: Hcg = Hxi + Hyj + Hzk Here, we have Hx = -Ixxωx Hy = Iyyωy Hz = -Iyzωy Express the position and velocity of the con in rectangular components, and determine the moment of the linear momentum of the con about the center of gravity of the sub: ρcon = dyj + dzk vcon = vxj + vyk Use Eq. 7 to determine the angular momentum of the con about the center of gravity of the sub: HA = ρcon × mcvcon + Hcg = (-Ixxωx - dzvy)i + (-Iyyωy - dzvx)j |
||
Practice Homework and Test problems now available in the 'Eng Dynamics' mobile app
Includes over 400 free problems with complete detailed solutions.
Available at the Google Play Store and Apple App Store.