| Ch 5. Rigid Body General Motion | Multimedia Engineering Dynamics | ||||||
| Fixed Axis Rotation | Plane Motion Velocities | Zero Velocity Point | Plane Motion Accelerations |
Multiple Gears |
Rot. Coord. Velocities | Rot. Coord. Acceleration | |
| General Plane Motion: Acceleration | Case Intro | Theory | Case Solution | Example |
| Chapter |
| - Particle - |
| 1. General Motion |
| 2. Force & Accel. |
| 3. Energy |
| 4. Momentum |
| - Rigid Body - |
| 5. General Motion |
| 6. Force & Accel. |
| 7. Energy |
| 8. Momentum |
| 9. 3-D Motion |
| 10. Vibrations |
| Appendix |
| Basic Math |
| Units |
| Basic Dynamics Eqs |
| Sections |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
|
|
|||||
|
|
Relative acceleration equation can be derived from the the relative velocity equation, vB = vA + vB/A Differentiate with respect to time to give dvB/dt =dvA/dt + dvB/A/dtJust like the relative velocity equation, the relative acceleration equation can be separated into linear motion and angular motion. However, it is important to note that the angular motion has two components, tangential and normal acceleration. |
||||
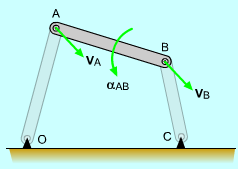 3-Bar Acceleration Motion |
Each rotation term can be written as cross products, giving aB = aA + ωAB × (ωAB × rAB) + αAB × rAB This form shows that the relative acceleration is composed of the translating motion of base point A and the rotating motion of point B about A. For plane motion, the normal rotation terms can be simplified as -ω2r giving aB = aA - ω2rAB + α × rAB Another way to write the relative acceleration equation is aB = aA - ω2ren + αret |
||||
Practice Homework and Test problems now available in the 'Eng Dynamics' mobile app
Includes over 400 free problems with complete detailed solutions.
Available at the Google Play Store and Apple App Store.

