| Ch 5. Rigid Body General Motion | Multimedia Engineering Dynamics | ||||||
| Fixed Axis Rotation | Plane Motion Velocities | Zero Velocity Point | Plane Motion Accelerations |
Multiple Gears |
Rot. Coord. Velocities | Rot. Coord. Acceleration | |
| General Plane Motion: Acceleration | Case Intro | Theory | Case Solution | Example |
| Chapter |
| - Particle - |
| 1. General Motion |
| 2. Force & Accel. |
| 3. Energy |
| 4. Momentum |
| - Rigid Body - |
| 5. General Motion |
| 6. Force & Accel. |
| 7. Energy |
| 8. Momentum |
| 9. 3-D Motion |
| 10. Vibrations |
| Appendix |
| Basic Math |
| Units |
| Basic Equations |
| Sections |
| Search |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| Author(s): |
| Kurt Gramoll |
| ©Kurt Gramoll |
|
|
||
 Sliding Piston |
Example |
|
|
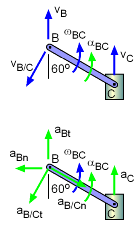
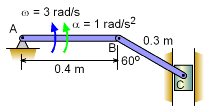
Two bars link a vertically sliding piston, C, to a pinned point, A. If bar AB rotates at a rate of 3 rad/s and accelerates at a rate of 1 m/s2, what is the angular acceleration of bar BC?
|
||
| Solution |
||
|
|
Velocity information about bar BC must first be found before accelerations can be determined. The key object in this system is rod BC. Velocity of points B can be found, and velocity direction of C can be found. Velocity The velocity direction of C is known, thus Combining gives, Acceleration Acceleration of point C, Combining, |
|
Practice Homework and Test problems now available in the 'Eng Dynamics' mobile app
Includes over 400 free problems with complete detailed solutions.
Available at the Google Play Store and Apple App Store.