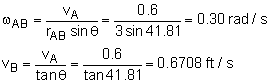| Ch 5. Rigid Body General Motion | Multimedia Engineering Dynamics | ||||||
| Fixed Axis Rotation | Plane Motion Velocities | Zero Velocity Point | Plane Motion Accelerations |
Multiple Gears |
Rot. Coord. Velocities | Rot. Coord. Acceleration | |
| General Plane Motion: Acceleration | Case Intro | Theory | Case Solution | Example |
| Chapter |
| - Particle - |
| 1. General Motion |
| 2. Force & Accel. |
| 3. Energy |
| 4. Momentum |
| - Rigid Body - |
| 5. General Motion |
| 6. Force & Accel. |
| 7. Energy |
| 8. Momentum |
| 9. 3-D Motion |
| 10. Vibrations |
| Appendix |
| Basic Math |
| Units |
| Basic Dynamics Eqs |
| Sections |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
|
|
||
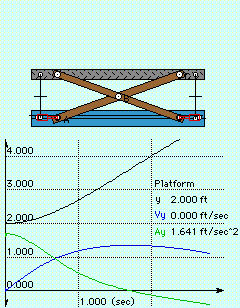
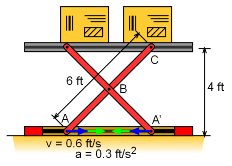 Problem Diagram |
The velocity needs to be determined before the acceleration can be calculated. The motion of the lift can be determined using the following conditions;
|
|
| Velocity of Point B |
||
|
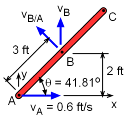
|
The geometric constraints of points A and B are critical in determining the member AC angular velocity. The velocity vectors for points A and B are vA = vAi vB = vBj The relative velocity equation for bar AB is vB = vA + vB/A vB = vA + ωAB × rAB vBj = vAi + ωABk × rAB (cosθi + sinθj) = vAi + ωAB rAB (cosθj - sinθi) Sum in both the i and j directions gives, j : vB = ωABrABcosθ i : vA = ωABrABsinθ There are only two unknowns, vA and ωAB, which can be solved for, giving The vertical velocities of points C and B are related by a factor of 2, giving, vC = 2vB = 1.33 ft/s |
|
| Acceleration of Point C |
||
|
|
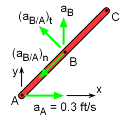
As with the velocity, the geometric constraints of points A and B are used to determine their acceleration direction, aA = aAi aB = aBj The relative acceleration equation for bar AB is aB = aA + aB/A = aA + (aB/A)n + (aB/A)t = aA + ωAB × (ωAB × rAB) + (αAB × rAB) aBj = aAi + ωABk × (ωAB k × rAB (cosθi +
sinθj)) aBj = aAi +
ω2AB rAB (-cosθi - sinθj)) Summing in both the i and j directions gives, i : 0 = aA - αABrABsinθ - ω2ABrABcosθ j : aB = αAB rAB cosθ - ω2ABrABsinθ |
|
|
|
These two equations can be used to solve for the two unknowns, αAB and aB. Solving for αAB in the first equation and then substituting into the second equation gives, Using numerical values give, αAB = 0.04938 rad/s2 aB = -0.06959 ft/s2 The vertical acceleration of the lift is twice the vertical acceleration of point B, alift = 2aB = -0.1392 ft/s2 |
|
Practice Homework and Test problems now available in the 'Eng Dynamics' mobile app
Includes over 400 free problems with complete detailed solutions.
Available at the Google Play Store and Apple App Store.