| Ch 4. Particle Momentum and Impulse | Multimedia Engineering Dynamics | ||||||
| Impulse & Momentum | Consv. Linear Momentum | Impact |
Angular Momentum |
Mass Flow |
|||
| Impact | Case Intro | Theory | Case Solution | Example |
| Chapter |
| - Particle - |
| 1. General Motion |
| 2. Force & Accel. |
| 3. Energy |
| 4. Momentum |
| - Rigid Body - |
| 5. General Motion |
| 6. Force & Accel. |
| 7. Energy |
| 8. Momentum |
| 9. 3-D Motion |
| 10. Vibrations |
| Appendix |
| Basic Math |
| Units |
| Basic Dynamics Eqs |
| Sections |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
|
|
|||||
|
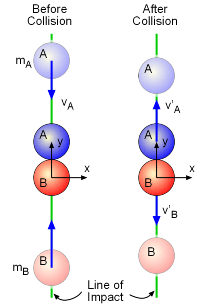
Consider two objects colliding with each other. If no external forces act on the objects before, after or during the collision, then total linear momentum before and after the impact is conserved. Thus, the conservation of linear momentum where v' represents the velocity after the impact, holds true for two object collisions. |
|||||
| Plastic Impact |
|||||
|
If the two objects adhere and remain connected after the impact, the impact is said to be perfectly plastic. Recall, from the Conservation of Linear Momentum section, if the velocity of each object is constant before the collision, the velocity of the combined center of gravity after the collision is Since the masses are combined after a plastic collision, there is only one unknown, v. No other equations are needed to solve for the velocity after the collision. |
|||||
| Direct Central Impact |
|||||
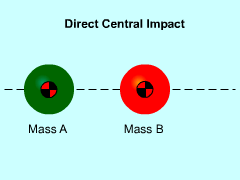 Direct Central Impact |
To keep things simple, first consider two objects that impact while traveling along the same straight line (1D collision). If the force that the objects exert on each other is parallel to the path of motion and directed towards the center of gravity of each object, the objects will undergo a direct central impact. After the impact, the objects will continue to travel along the same straight line but each object can have a different velocity. These means there are two unknowns and only one equation (linear momentum equation given above). To solve this type of problem, the Coefficient of Restitution for the collision needs to be used. This is discussed below |
||||
| Coefficient of Restitution |
|||||
|
|
If the impact between two objects does not result in a plastic collision, two equations are required to solve for the velocity of each object after the impact. During the impact, each object can lose energy (for a variety of reasons, e.g. sound or heat). This loss in energy can be expressed as the difference in velocity after the collision divided by the difference in velocity before the collision, or The prime velocities, vB' and vA' are velocities after the collision. The coefficient of restitution is a measure of the energy that is lost during a collision. For a perfectly elastic collision (e = 1), no energy is lost. The Coefficient of Restitution for small rubber balls is very close to one, which makes them very bouncy and fun to play with. One other important issue with the Coefficient of Restitution equation is that it is only applicable in the direction of the impact (referred to as the Line of Impact). Coefficient of Restitution is a scalar and cannot be used tangent to the Line of Impact. |
||||
| Oblique Central Impact |
|||||
|
|
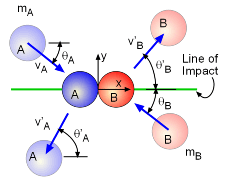
The more complex problem involves two objects moving in different directions. This type of problem involves four unknowns, direction and speed of each object after the collision. First, consider two objects that impact with arbitrary velocities, vA and vB, at an arbitrary angles, θA and θB, while traveling in the x-y plane. It is assumed that the force that the objects exert on each other is parallel to the Line of Impact (the x axis in the diagram at the left). Also, all impact forces are assumed to act through the center of mass of each object. |
||||
The velocities in the y direction (and z direction if a 3D collision) do not change after the impact since they are perpendicular to the Line of Impact, v'Ay = vAy v'By = vBy These two relationships are critical in solving oblique central impact problems since there are four unknowns. The other two required equations are the linear momentum in the direction of the Line of Impact, mAvAx + mBvBx = mAv'Ax + mBv'Bx and, of course, the Coefficient of restitution in the Line of Impact, |
|||||
Practice Homework and Test problems now available in the 'Eng Dynamics' mobile app
Includes over 400 free problems with complete detailed solutions.
Available at the Google Play Store and Apple App Store.