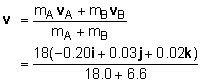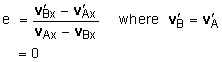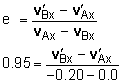| Ch 4. Particle Momentum and Impulse | Multimedia Engineering Dynamics | ||||||
| Impulse & Momentum | Consv. Linear Momentum | Impact |
Angular Momentum |
Mass Flow |
|||
| Impact | Case Intro | Theory | Case Solution | Example |
| Chapter |
| - Particle - |
| 1. General Motion |
| 2. Force & Accel. |
| 3. Energy |
| 4. Momentum |
| - Rigid Body - |
| 5. General Motion |
| 6. Force & Accel. |
| 7. Energy |
| 8. Momentum |
| 9. 3-D Motion |
| 10. Vibrations |
| Appendix |
| Basic Math |
| Units |
| Basic Dynamics Eqs |
| Sections |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
|
|
||
| Plastic Impact - Solution part a) |
||
|
|
If the docking is successful, then the ships remain together, and the impact is perfectly plastic. Use the Conservation of Linear Momentum to solve for the velocity of the combined vehicles after the impact: = -0.146i + 0.022j + 0.015k m/s Although not needed for the plastic impact solution, it is interesting to note that for a perfectly plastic collision, the coefficient of restitution is zero. |
|
| Elastic Impact - Solution part b) |
||
|
|
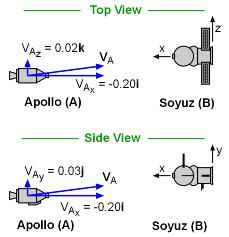
If the docking is not successful, and the force of the impact is directed along the x-axis, then the collision is an oblique central impact. Since the force is only along the x-axis, then the Line of Impact will also be the x-axis. This also means that the y and z components of the velocity and momentum of each ship remain unchanged after the impact. vAy = v'Ay = 0.03 m/s vAz = v'Az = 0.02 m/s Apply the conservation of linear momentum in the x direction, gives,
18.0 (-0.2) = 18.0 v'Ax + 6.6 v'Bx This has two unknown, so a second equation or relationship is needed. Use the coefficient of restitution, Solvign the two equations simultaneously gives, v'Ax = -0.095 v'Bx = -0.285 Putting all values together gives, vAx = -0.095i + 0.03j + 0.02k m/s vBx = -0.285i m/s |
|
Practice Homework and Test problems now available in the 'Eng Dynamics' mobile app
Includes over 400 free problems with complete detailed solutions.
Available at the Google Play Store and Apple App Store.