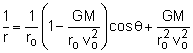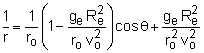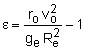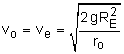| Ch 2. Particle Force and Acceleration | Multimedia Engineering Dynamics | ||||||
|
Rect. Coord. |
Normal/Tang. Coord. |
Polar Coord. |
Orbital Mechanics | Computational Mechanics | |||
| Orbital Mechanics | Case Intro | Theory | Case Solution | Example |
| Chapter |
| - Particle - |
| 1. General Motion |
| 2. Force & Accel. |
| 3. Energy |
| 4. Momentum |
| - Rigid Body - |
| 5. General Motion |
| 6. Force & Accel. |
| 7. Energy |
| 8. Momentum |
| 9. 3-D Motion |
| 10. Vibrations |
| Appendix |
| Basic Math |
| Units |
| Basic Dynamics Eqs |
| Sections |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
|
|
||||||||
|
Using polar coordinates, equations that describe the orbital trajectory of a satellite or planet can be derived. |
||||||||
|
|
||||||||
| Central Force Motion |
||||||||
 Central Force Motion |
If a particle moves under the influence of a force that is directed toward a fixed point, the particle is said to be in central force motion (CFM). CFM is commonly caused by electrostatic or gravitational forces. A satellite orbiting a planet, for example, exhibits CFM. As the satellite orbits the planet, the magnitude and direction of both the velocity and force change, but the force is always in the direction of the planet. Basically, the satellite is always accelerating towards the planet, but due to its sideways velocity, it stays in orbit. The general force equilibrium equation is extremely simple since the only force acting on the satellite is gravity, F = GMm/r2 where G is the Gravitation Constant (not 'g'), M is the mass of the central body, and m is the mass of the satellite. For earth, Ge = 66.73×10-12 m3/(kg-s2) and Me = 5.9×1030 kg. |
|||||||
| Kepler's 2nd Law |
||||||||
 Kepler's 2nd Law |
Before presenting the basic equation of motion for orbits, it is important to understand Kepler's 2nd Law. In the θ direction of orbits (polar coordinates), there is no force, giving, This requires r vθ to be a constant, or Another way to derive this is with conservation of angular momentum. Note, the velocity in the θ direction is not always tangent to the orbit except for circular orbits (see diagram below). |
|||||||
| Earth Satellite Motion
|
||||||||
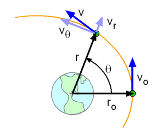 Position and Velocity Definition of a CFM satellite |
The general equilibrium equation above is actually a second order differential equation that can be solved. This section will concentrate on the basic motion of a satellite orbiting the earth when the satellite mass is negligible when compared to the earth. To set the boundary condition, consider a satellite at time t = 0, at a distance ro from the center of the earth, with a velocity vo parallel to the tangent of the earth's surface as shown. Then the complete general solution is (derivation omitted), |
|||||||
|
|
But, 'G' is not a convenient constant for engineers. The equation can be convert to 'g' using the GM = gR2, where Re is the radius of the earth, 6,370 km or 3,960 mi. This form can be used for other planets, but both R and g will have different constants. There is a more convenient format when the eccentricity definition of conic sections (see section below) is used,
where ge = 9.81 m/s2 or 32.2 ft/s2. After some algebraic rearranging, the central force equation can be written as,
|
|||||||
| Conic Sections |
||||||||
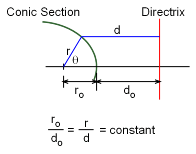
|
|
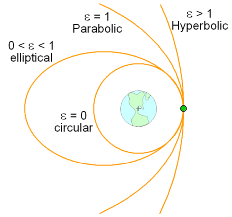
From analytical geometry, a conic section is a curve that has the property that the ratio of the radius r to the perpendicular distance to a straight line d (called the directrix) is constant. The ratio r/d = ro/do is called the eccentricity. From the figure one can see that r cosθ + d = ro + do This can be written in terms of the eccentricity as Comparing this with the first equation above, it is seen that the satellite's free-flight trajectory describes a conic section with eccentricity ε. The type of trajectory taken by the satellite is determined by the value of ε. There are four types of trajectories to consider. |
|||||||
| Circular Trajectory (ε = 0) |
||||||||
|
If vo is chosen such that ε = 0, then r must equal ro, and the trajectory is circular. Setting ε = 0, the velocity for a circular trajectory can be determined as |
||||||||
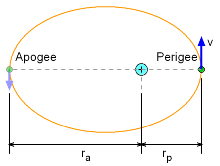
| Elliptical Trajectory (0 < ε < 1) |
||||||||
|
|
If 0 < ε < 1, the trajectory is elliptical. The minimum radius, or radius at perigee rp, occurs at θ = 0°. Thus, the initial radius is the radius at perigee, ro = rp The maximum radius, or radius at apogee ra, occurs at θ = 180°. Setting θ = 180° gives Notice that the maximum radius increases without limit as e approaches 1. |
|||||||
| Parabolic Trajectory (ε = 1) |
||||||||
| When ε = 1, the trajectory is
parabolic, which means that the initial velocity vo is the
escape velocity ve.
Setting ε = 1, gives
|
||||||||
| Hyperbolic Trajectory (ε > 0) |
||||||||
| For ε > 1, the trajectory is hyperbolic and is not directly applicable to standard earth orbits. | ||||||||
Practice Homework and Test problems now available in the 'Eng Dynamics' mobile app
Includes over 400 free problems with complete detailed solutions.
Available at the Google Play Store and Apple App Store.