| Ch 5. Rigid Body General Motion | Multimedia Engineering Dynamics | ||||||
| Fixed Axis Rotation | Plane Motion Velocities | Zero Velocity Point | Plane Motion Accelerations |
Multiple Gears |
Rot. Coord. Velocities | Rot. Coord. Acceleration | |
| General Plane Motion: Acceleration | Case Intro | Theory | Case Solution | Example |
| Chapter |
| - Particle - |
| 1. General Motion |
| 2. Force & Accel. |
| 3. Energy |
| 4. Momentum |
| - Rigid Body - |
| 5. General Motion |
| 6. Force & Accel. |
| 7. Energy |
| 8. Momentum |
| 9. 3-D Motion |
| 10. Vibrations |
| Appendix |
| Basic Math |
| Units |
| Basic Dynamics Eqs |
| Sections |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
|
|
||
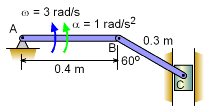 Sliding Piston |
Example |
|
|
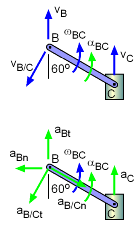
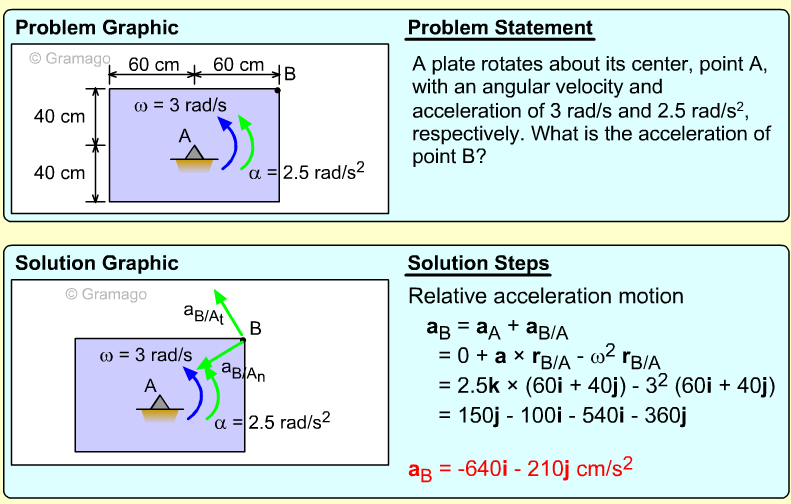
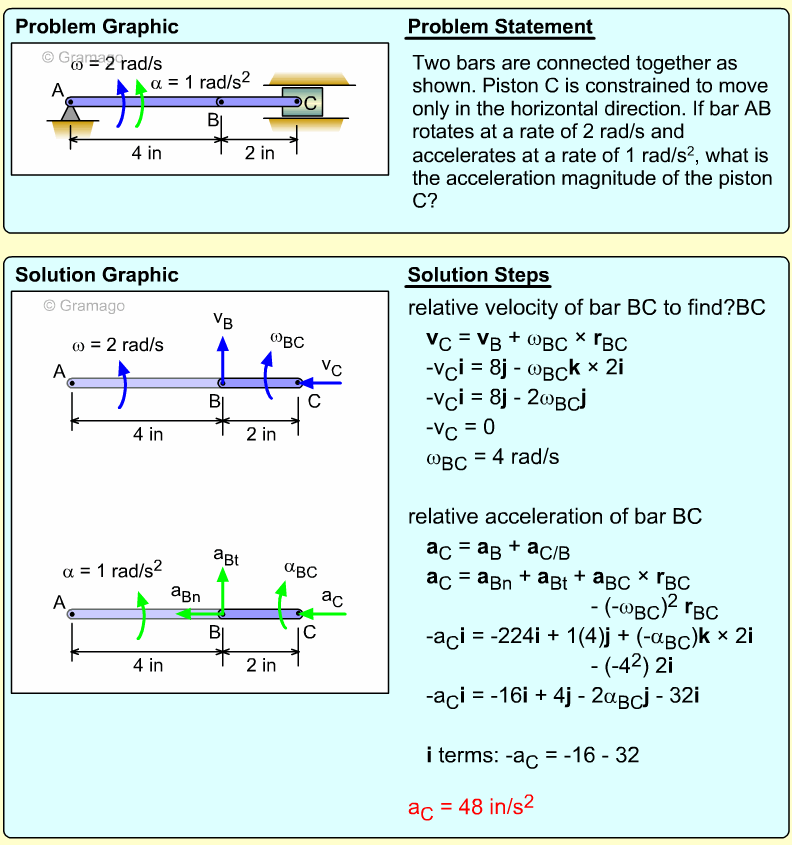
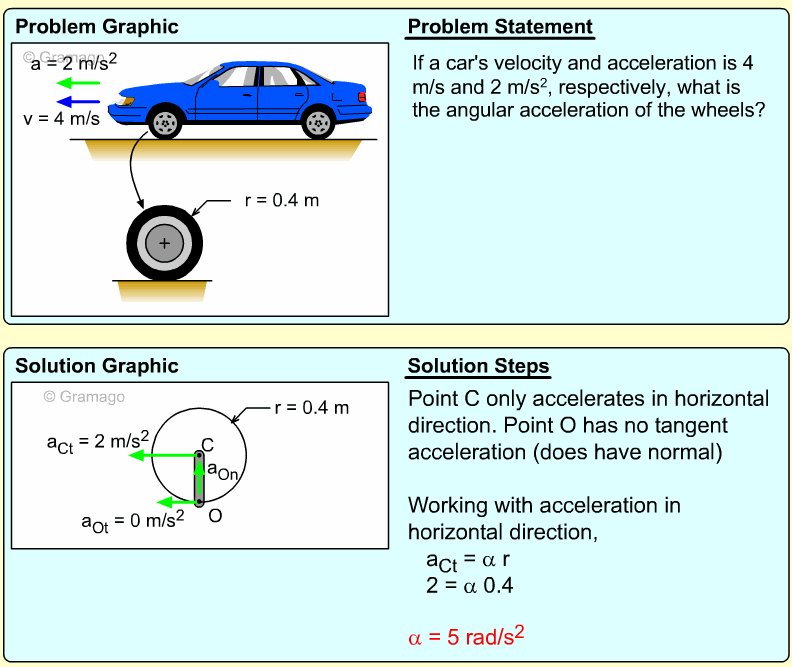
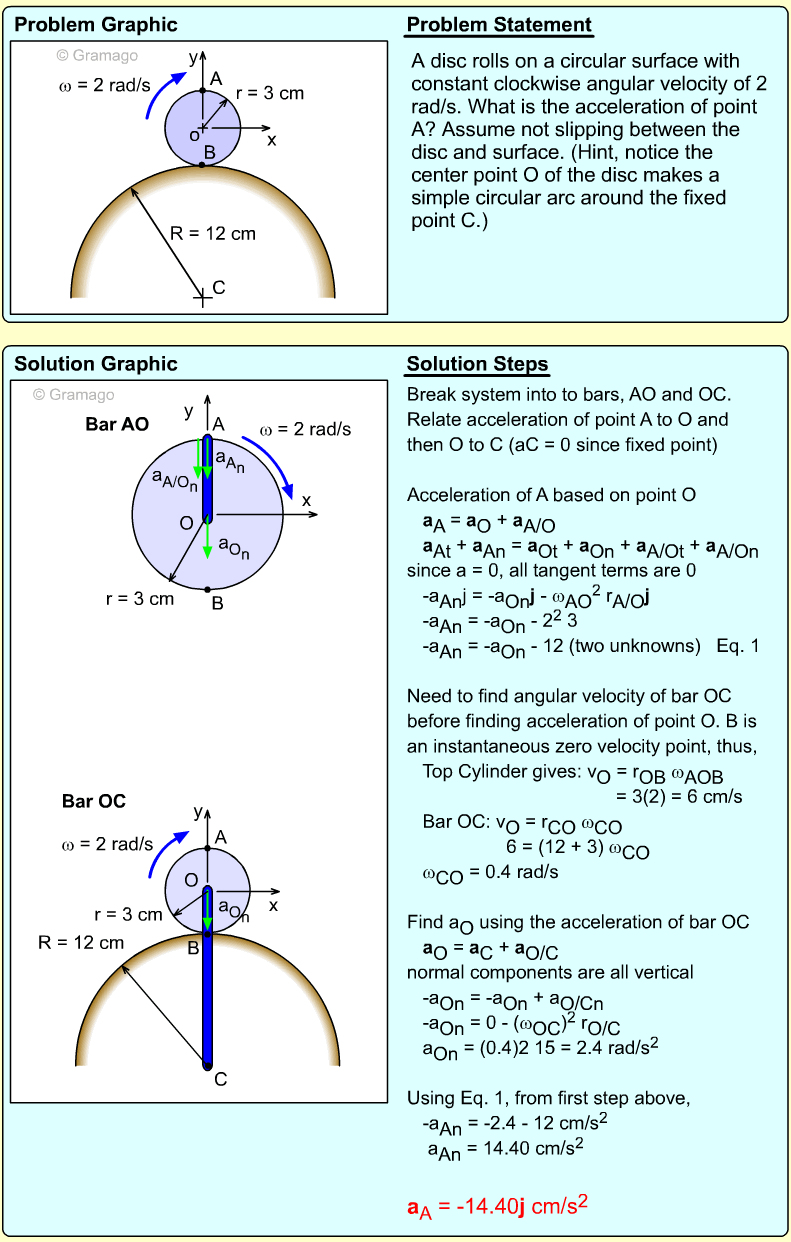
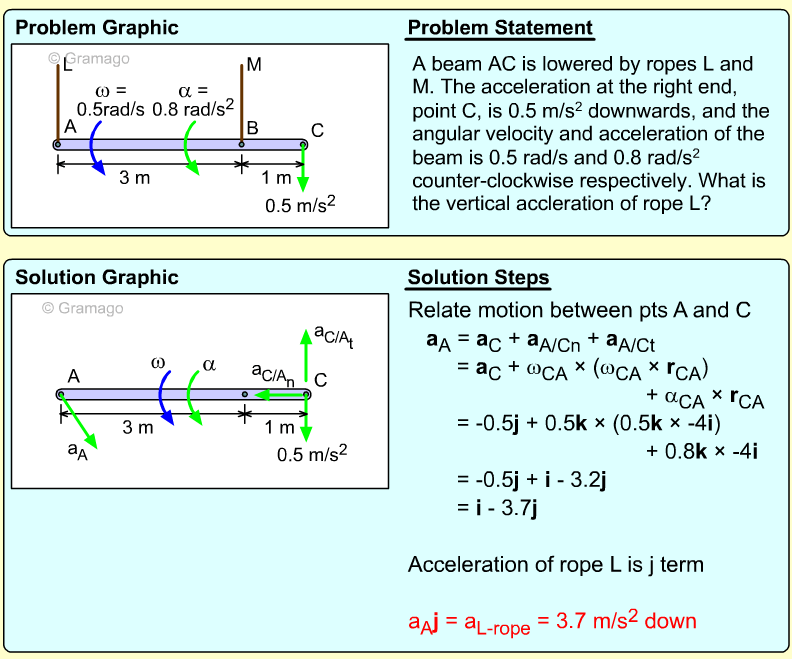
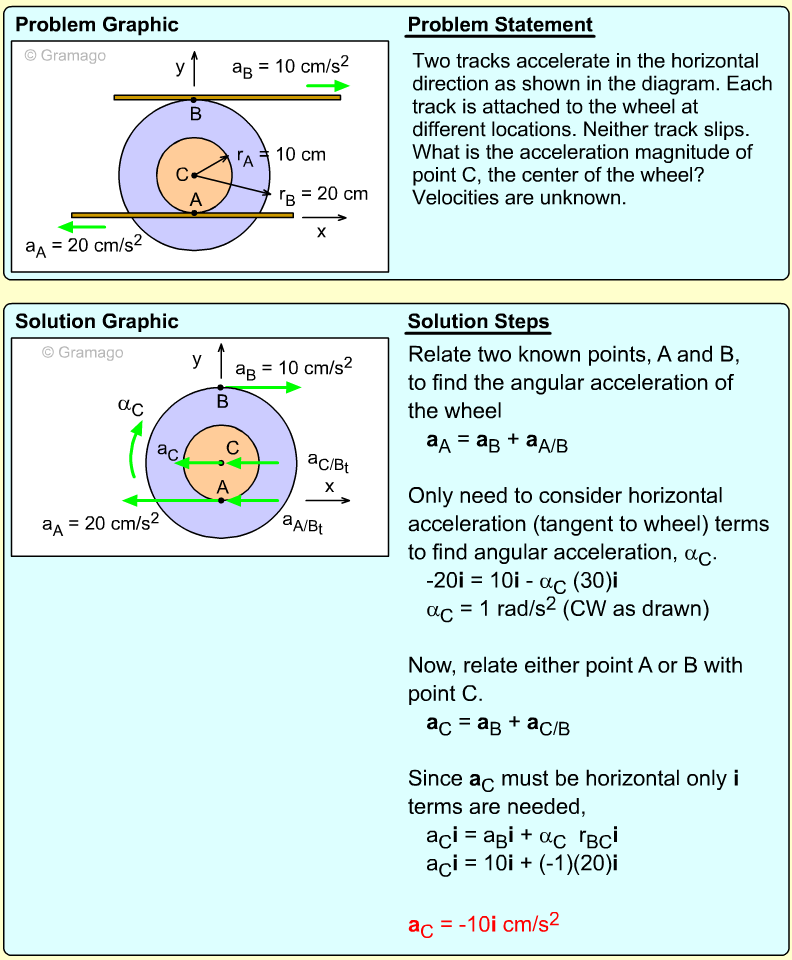
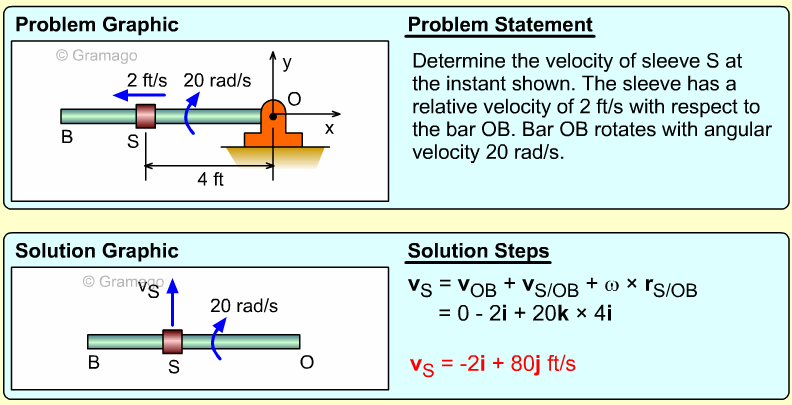
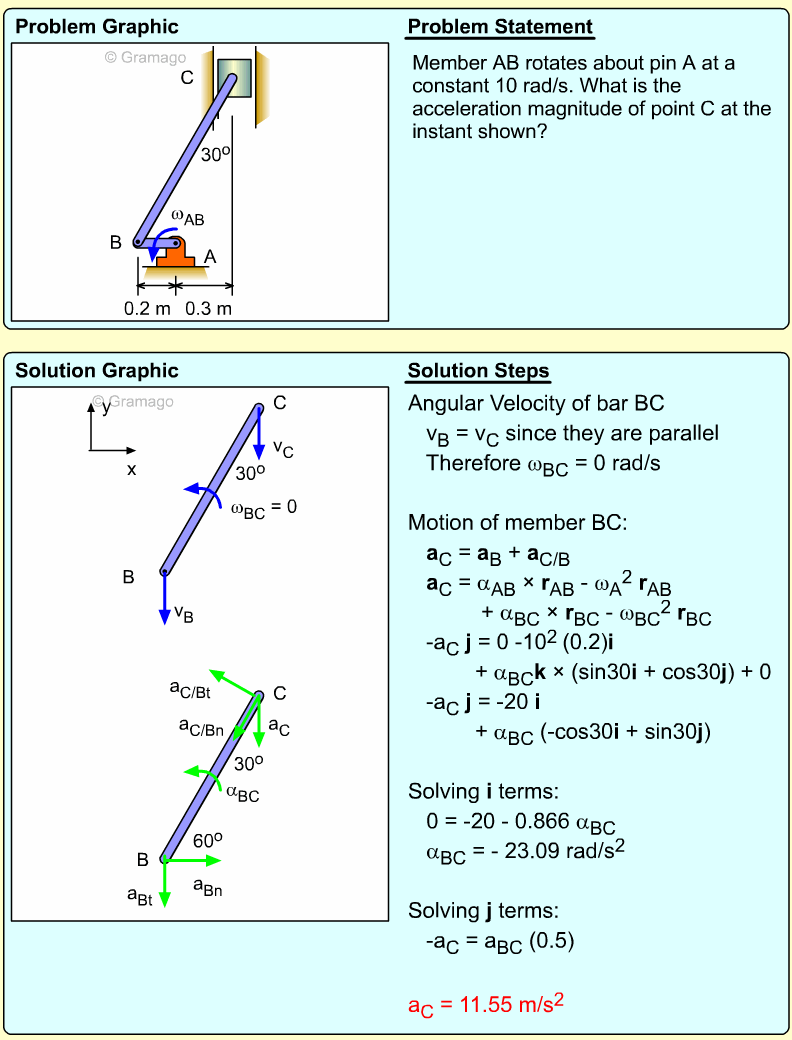
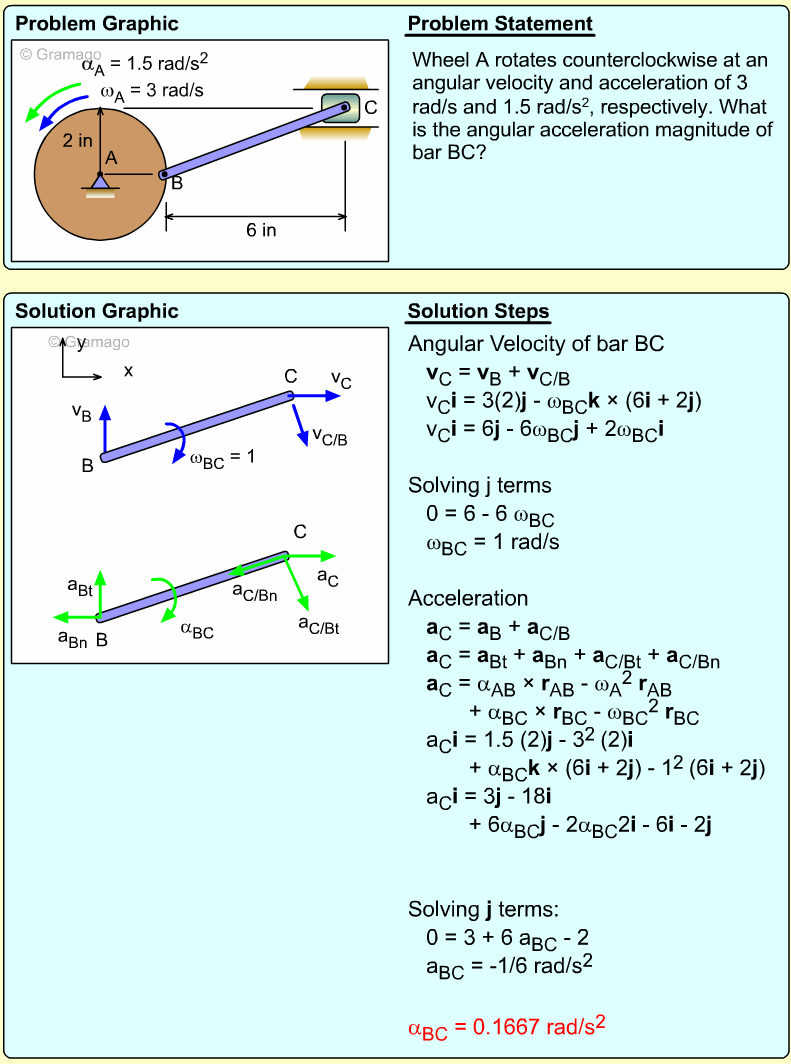
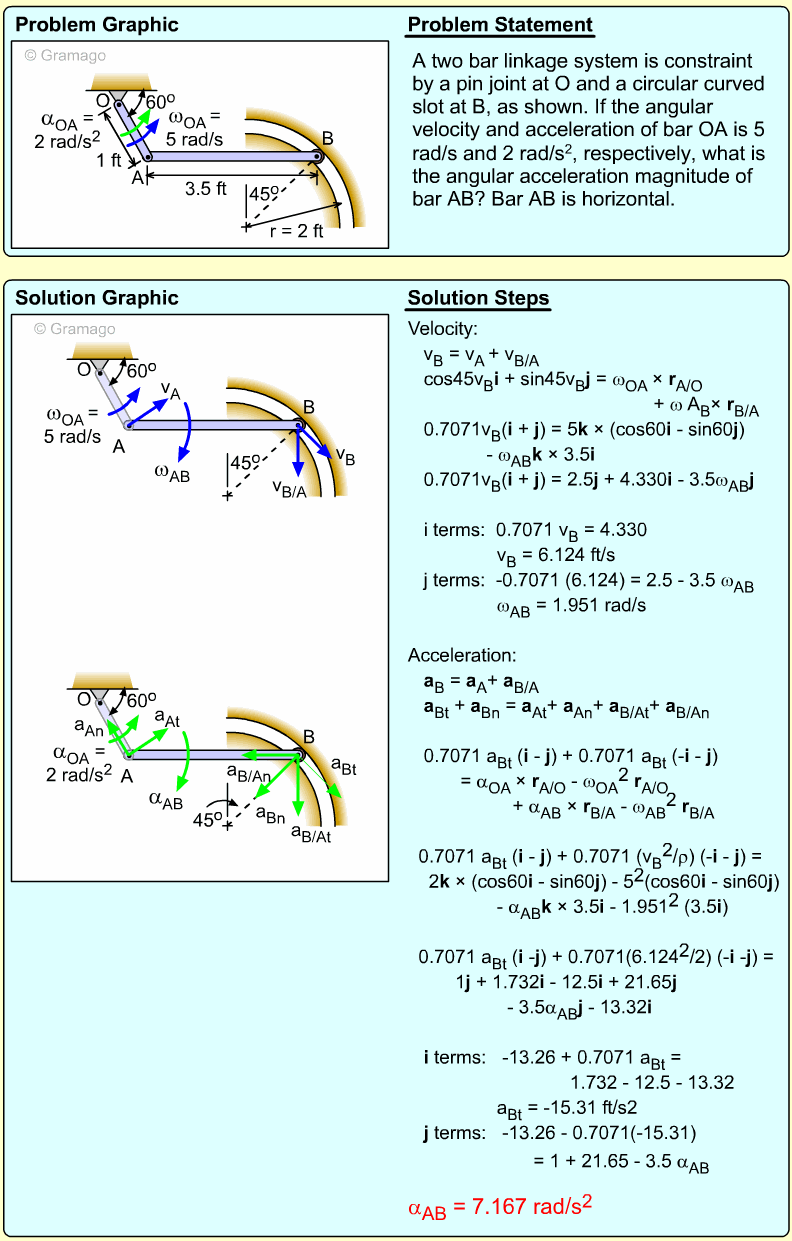
Two bars link a vertically sliding piston, C, to a pinned point, A. If bar AB rotates at a rate of 3 rad/s and accelerates at a rate of 1 m/s2, what is the angular acceleration of bar BC?
|
||
| Solution |
||
|
|
Velocity information about bar BC must first be found before accelerations can be determined. The key object in this system is rod BC. Velocity of points B can be found, and velocity direction of C can be found. Velocity The velocity direction of C is known, thus Combining gives, Acceleration Acceleration of point C, Combining, |
|
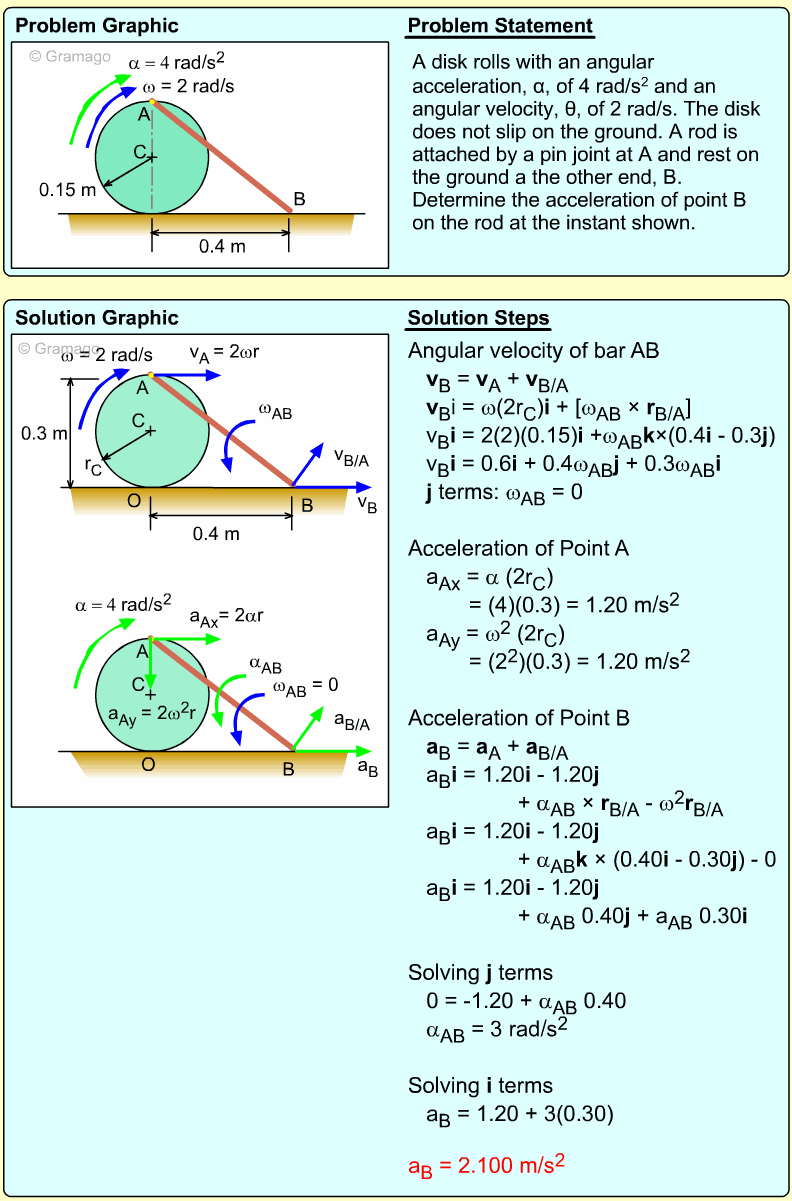
| Example Problem 1 |
||
|
||
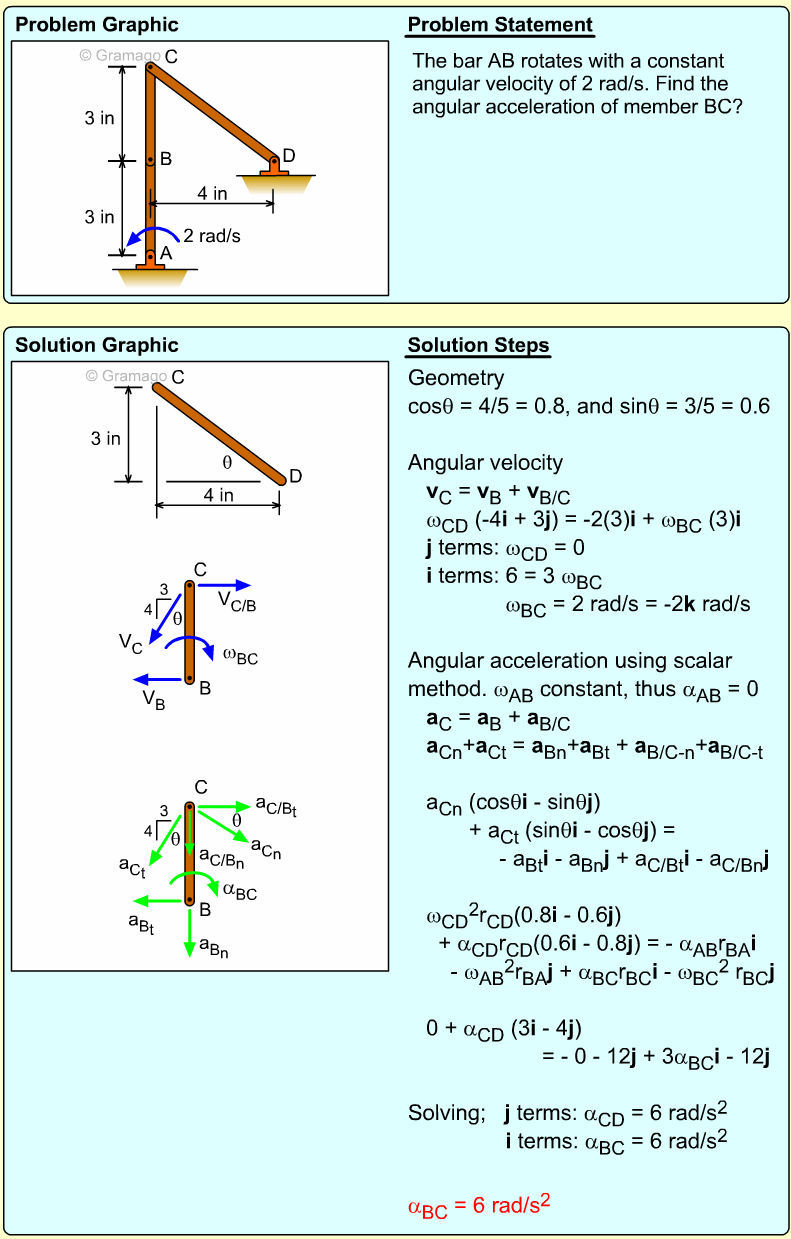
| Example Problem 2 |
||
|
||
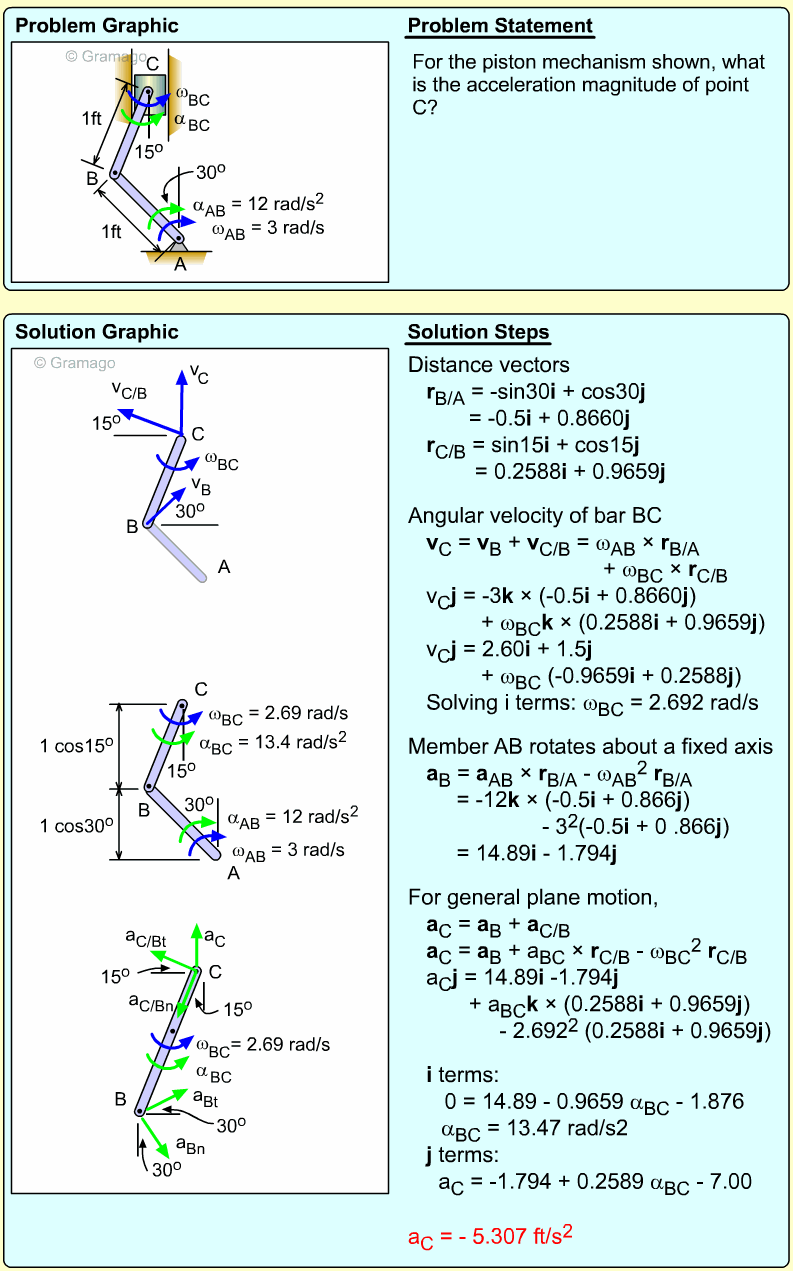
| Example Problem 3 |
||
|
||
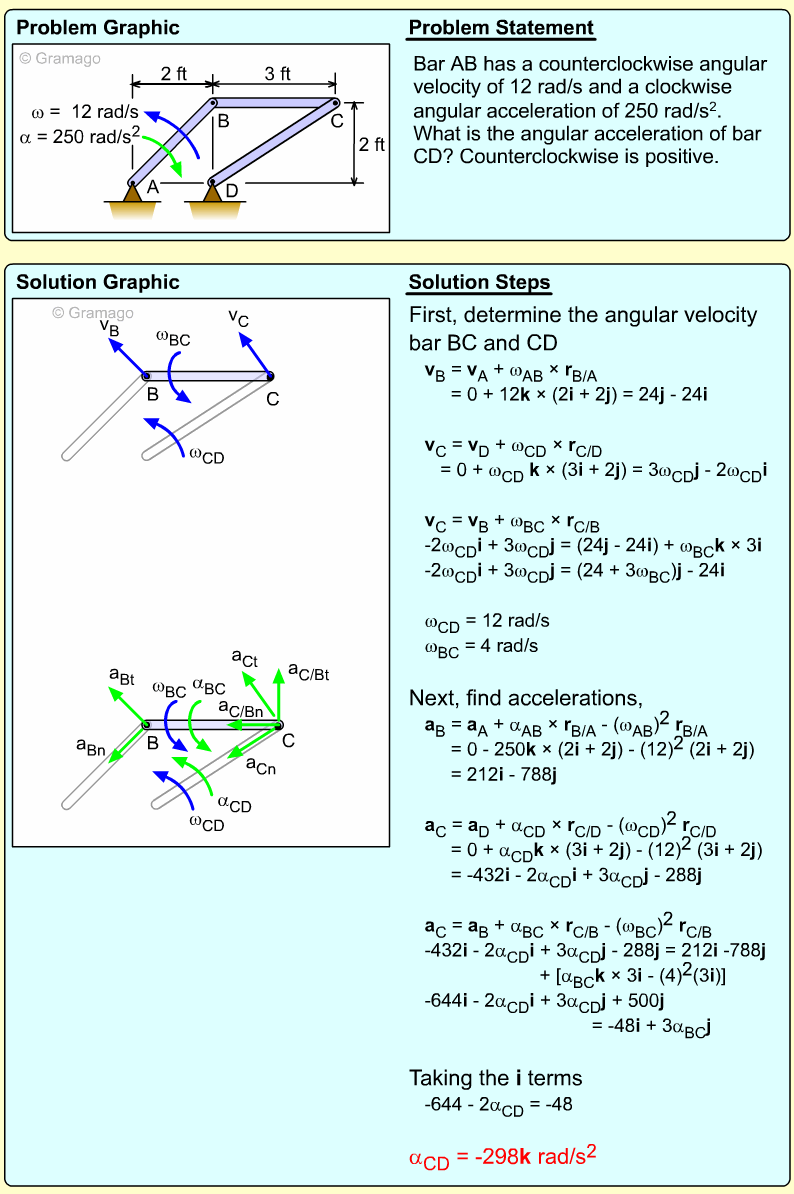
| Example Problem 4 |
||
|
||
| Example Problem 5 |
||
|
||
| Example Problem 6 |
||
|
||
| Example Problem 7 |
||
|
||
| Example Problem 8 |
||
|
||
| Example Problem 9 |
||
|
||
| Example Problem 10 |
||
|
||
| Example Problem 11 |
||
|
||
| Example Problem 12 |
||
|
||
| Example Problem 13 |
||
|
||
| Example Problem 14 |
||
|
||
| Example Problem 15 |
||
|
||
| Example Problem 16 |
||
|
||
| Example Problem 17 |
||
|
||
| Example Problem 18 |
||
|
||
| Example Problem 19 |
||
|
||
| Example Problem 20 |
||
|
||
| Example Problem 21 |
||
|
||
| Example Problem 22 |
||
|
||