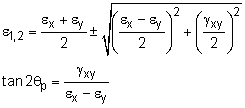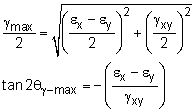| Ch 8. Strain Analysis | Multimedia Engineering Mechanics | ||||||
|
Plane Strain |
Mohr's Circle for Strain |
Strain Gages |
|||||
| Plane Strain and Principal Strains | Case Intro | Theory | Case Solution | Example |
| Chapter |
| 1. Stress/Strain |
| 2. Torsion |
| 3. Beam Shr/Moment |
| 4. Beam Stresses |
| 5. Beam Deflections |
| 6. Beam-Advanced |
| 7. Stress Analysis |
| 8. Strain Analysis |
| 9. Columns |
| Appendix |
| Basic Math |
| Units |
| Basic Mechanics Eqs |
| Sections |
| Material Properties |
| Structural Shapes |
| Beam Equations |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
|
|
|||||
|
|
Strain Element |
||||
|
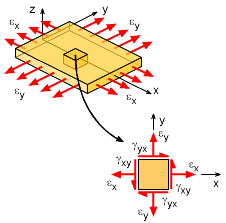
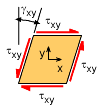
Similar to stress analysis at a point, strain can also be rotated to different directions and thus maximum shear and normal strains can be found. Strain at a given point on a two dimensional object can be seen as a small strain element with two normal strains and one shear strain, as shown in the diagram. The sign convention for strains at a point is similar to stresses at a point. Normal tension strain in both the x and y direction are assumed positive. The positive shear strain direction is shown in the diagram at the left. Shear stresses act on four sides of the stress element, causing a pinching or shear action. Shear strains on all four sides are the same, thus γxy = γyx Recall, the shear strain is actually defined as the angle of rotation or twist due to the shear stress. This angle is in radians and is shown at the left. |
|||||
| Strain Rotation |
|||||
|
|
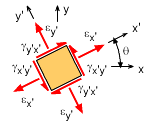
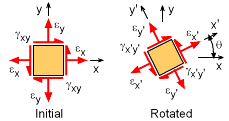
Stains at a point (strain element) can be rotated to give a new strain state at any particular angle. The rotation angle, θ, is assumed positive using the right hand rule (counter-clockwise in the x-y plane is positive). The new coordinate system is labeled as x' and y'. The new rotated strains are shown in the diagram at the left. The shear strains, γx'y' and γy'x' are still equal. As one may expect, the strain transformation equations are nearly identical to the stress transformation angles. The only difference is a factor of 2 for the shear strain. Other than that, the strain symbol, ε, can be simply substituted for σ to give the strain transformation equations (detail derivation is omitted). The final equations are,
|
||||
| Principal Strains |
|||||
|
Generally, the largest normal strain is of most interest. This can be found by taking a derivative of either the εx´ or εy´ strain with respect to θ and equating it to zero. This will give the principal rotation angle, θp, that will produce the principal (maximum and minimum) strains. The resulting equations are
These strains, ε1 or ε2 are referred to as the principal shear strains. |
|||||
 Plot of Rotated Strain |
Maximum Shear Strain |
||||
|
Similar to the principal strains, the maximum shear strain can be determine by taking a derivative of γx´y´ strain with respect to θ and equating it to zero. This gives
|
|||||
Practice Homework and Test problems now available in the 'Eng Mechanics' mobile app
Includes over 500 free problems with complete detailed solutions.
Available at the Google Play Store and Apple App Store.