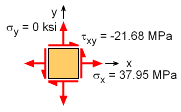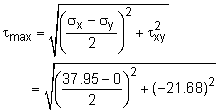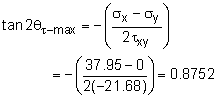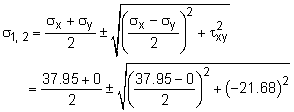| Ch 7. Stress Analysis | Multimedia Engineering Mechanics | ||||||
|
Plane Stress |
Principal Stresses |
Mohr's Circle for Stress |
Failure |
Pressure Vessels |
|||
| Principal and Max. Shear Stresses | Case Intro | Theory | Case Solution | Example |
| Chapter |
| 1. Stress/Strain |
| 2. Torsion |
| 3. Beam Shr/Moment |
| 4. Beam Stresses |
| 5. Beam Deflections |
| 6. Beam-Advanced |
| 7. Stress Analysis |
| 8. Strain Analysis |
| 9. Columns |
| Appendix |
| Basic Math |
| Units |
| Basic Mechanics Eqs |
| Sections |
| Material Properties |
| Structural Shapes |
| Beam Equations |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
|
|
||
|
|
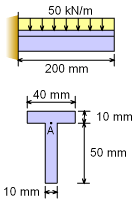
Before the stress state at point A can be analyzed for maximum shear and normal stresses, the maximum bending moment and shear load in the beam needs to be determined. From the maximum bending moment, the maximum bending stress can be found. Also, from the maximum shear load, the maximum shear stress can be determined. Both of these stresses are in the beam oriented coordinate system. After bending and shear stresses are found, the stress element can be rotated to given the absolute maximum shear stress. This stress state will most likely be something other than the natural beam coordinate system. There are a number of preliminary steps required to find both the beam shear stress and bending stress. These include determining the moment-shear diagram, the neutral axis, moment of inertia, I, and the first moment of the area, Q. |
|
| Moment -Shear Diagrams |
||
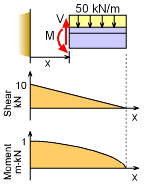 Shear-Moment Diagrams |
To find the maximum bending moment and shear load, the moment and shear equations can be used. Cutting the structure and summing the forces and moments, gives, ΣFy = 0 = V - 50(0.2 - x) V = (10 - 50x) kN and ΣM = 0 = M - 50 (0.2 - x) (0.2 - x)/2 M = (1 - 10 x + 25 x2) kN-m The maximum shear and moment will be at the wall, Vmax = 10 kN and Mmax = 1 kN-m |
|
| Neutral Axis and Moment of Inertia |
||
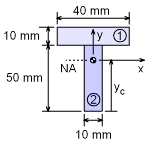 Neutral Axis Location |
The neutral axis is critical in finding the cross section moment of inertia and the first moment of the area. The moment of inertia for full cross section is, I = I1 + y12 A1 + I2 + y22 A2 = 40(10)3/12 + (50 - 38.33 + 10/2)2(40)(10) = 307,500 mm4 = 3.075 × 10-7 m4 |
|
| First Moment of the Area, Q |
||
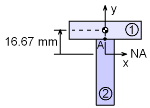 First Moment of Area 1 |
The first moment of the area, Q, is needed to determine the shear stress at point A. The area below or above point A can be used to calculate Q. If the area above is used, then Q is Q = y1A1 = (50 - 38.33 + 10/2)(40)(10) |
|
|
|
||
| Normal and Shear Stress at the Wall (at Point A) |
||
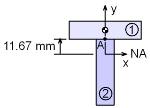 Distance from NA to Point A |
The maximum moment and shear occur at the wall and thus the maximum stresses will also occur at the wall. The normal stress at point A is σb = My/I The shear stress at A, is |
|
| Maximum Shear Stress |
||
|
|
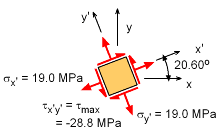
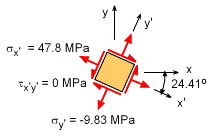
The bending stress and shear stress at point A is shown on a stress element at the left. The bending stress is considered to be acting in the x direction. There is no normal vertical stress, so σy is zero. The shear stress is acting down on the right edge of the stress element. Thus, the stress is negative and the shear stress on the right edge is drawn in the up direction. The maximum shear stress is This occurs at an angle of The rotated normal stresses are equal when the shear stress is a maximum, giving σx′ = σy′ = (σx + σy)/2 = 37.95/2 = 18.98 MPa All rotated stresses are labeled on the stress element at the left. Notice, the shear stress is actually negative when the shear stress rotation equation is used. On the other hand, the maximum shear stress equation above can be either positive or negative due to the square root. |
|
| Maximum Normal Stresses |
||
|
|
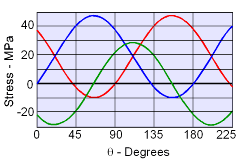
The maximum normal stress, or principal stresses σ1 and σ2, are This occurs at an angle of θp = -24.41o It is interesting to visualize the stresses for any angle by plotting the stresses as a function of θ. This is shown in the diagram at the left. Note, the stresses have a period of π, or 180o. This is due to the symmetric nature of the stresses. |
|
Practice Homework and Test problems now available in the 'Eng Mechanics' mobile app
Includes over 500 free problems with complete detailed solutions.
Available at the Google Play Store and Apple App Store.