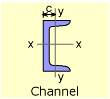| Ch 4. Beam Stresses | Multimedia Engineering Mechanics | ||||||
|
Bending Strain and Stress |
Beam Design |
Shear Stress |
Built-up Beams |
||||
| Beam Design | Case Intro | Theory | Case Solution | Example |
| Chapter |
| 1. Stress/Strain |
| 2. Torsion |
| 3. Beam Shr/Moment |
| 4. Beam Stresses |
| 5. Beam Deflections |
| 6. Beam-Advanced |
| 7. Stress Analysis |
| 8. Strain Analysis |
| 9. Columns |
| Appendix |
| Basic Math |
| Units |
| Basic Mechanics Eqs |
| Sections |
| Material Properties |
| Structural Shapes |
| Beam Equations |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
|
|
||||||||||||||||||
 Beam with Same Area but Different Load Capacity Due to Different I |
The geometric cross section is critical in beam design. For example, a solid rectangular cross section will support substantially less load than an efficient I-beam. The reason for this can be understood by examining the bending stress equation, σ = My/I. As I becomes large, the stress reduces. Thus, it is advantageous to have most of the cross-sectional area away from the x-axis which increases I. A good example of this is an I-beam. However, too much of a good thing is bad. For example, with an I beam, if the web section is too thin, shear stress will cause failure. |
|||||||||||||||||
| Section Modulus |
||||||||||||||||||
|
In the bending stress equation, there are two parameters, y and I, that are based on the cross section geometry. It would be easier to design beams if these two values were combined into a single parameter as S = I/c where c is the maximum y value (top or bottom edge) and S is the section modulus. The bending stress equation then changes to
|
||||||||||||||||||
|
The S value, the section modulus, is listed in handbooks for all major structural shapes (see Structural Shapes appendix). Thus, if the moment and allowable stress are known, then a structural member can be chosen that meets or exceeds the section modulus. This eliminates working with the moment of inertia and the distance from the neutral axis to the outside edge. |
|||||||||||||||||
| Structural Steel Shapes |
||||||||||||||||||
|
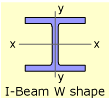
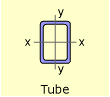
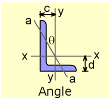
There are a large variety of structural shapes. The major ones include I-beams (W and S types), channels, tubes, angles, pipes, and tees. The I-beam is generally the most efficient, but may not fit the space or needs of a particular structure. Many times, structural shapes are combined, such as two angles, to give new shapes. One note of interest is that there are two I-beam types, W and S shapes. The S or Standard beam is narrower than the W or Wide-flange beam and was the first standardized I-beam sections. With the increased quality of steel and manufacturing techniques, the W beams have largely displaced the S beams. All the major shapes are shown at the left. Each one can be clicked and a list of popular shapes will be shown. |
||||||||||||||||||
| Lumber Shapes (US Units only) |
||||||||||||||||||
|
For various reasons, actual lumber dimensions (net) are not the same as the name (nominal) dimension. For example, a "2x4" is not 2 in by 4 in. It is important that the correct size be considered when designing any structure with wood. An additional issue with lumber is the inconsistent quality. Unlike metals that are manufactured, wood is natural which introduces a higher variation of stiffness and strength. Most handbooks that give material properties for wood use low values, but the design should also consider using a higher factor of safety. |
|||||||||||||||||
Practice Homework and Test problems now available in the 'Eng Mechanics' mobile app
Includes over 500 free problems with complete detailed solutions.
Available at the Google Play Store and Apple App Store.