| Ch 4. Beam Stresses | Multimedia Engineering Mechanics | ||||||
|
Bending Strain and Stress |
Beam Design |
Shear Stress |
Built-up Beams |
||||
| Beam Design | Case Intro | Theory | Case Solution | Example |
| Chapter |
| 1. Stress/Strain |
| 2. Torsion |
| 3. Beam Shr/Moment |
| 4. Beam Stresses |
| 5. Beam Deflections |
| 6. Beam-Advanced |
| 7. Stress Analysis |
| 8. Strain Analysis |
| 9. Columns |
| Appendix |
| Basic Math |
| Units |
| Basic Mechanics Eqs |
| Sections |
| Material Properties |
| Structural Shapes |
| Beam Equations |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
|
|
||
|
|
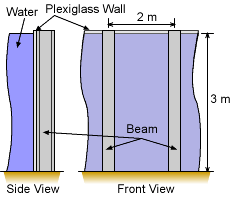
A new aquarium plans a large fish tank with a water depth of 3 meters. One of the walls will be constructed from Plexiglas and supported by vertical I-beams. The beams will be spaced every 2 meters. The water pressure will cause a distributed load on the beams. The beams can be modeled as a cantilever beams since the base is fixed and the top end is free. The minimum weight S type I-beam needs to be specified using the beams listed in the appendix. |
|
| Loading |
||
|
|
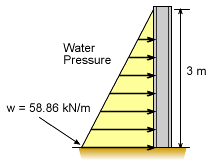
The water will cause a pressure on the wall which is a linear function of the depth. The pressure on the wall will be p = h g ρ where ρ is the water density and g is the gravitational constant, 9.81 m/s2. The maximum pressure will be at the bottom, h = 3 m, p = (3 m) (9.81 m/s2) (1 g/cm3) = (3 m) (9.81 kN/m3) = 29.43 kN/m2 The pressure now needs to be converted to a distributed load on a typical vertical beam. There is one beam for every 2 meters, so the maximum distributed load at the bottom is wmax = (29.43 kN/m2 )(2 m) = 58.86 kN/m |
|
| Moment |
||
|
|
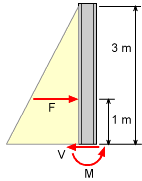
The maximum moment for a cantilever beam is at the base. The distributed load has an equivalent load of F = 0.5 (58.86 kN/m)(3 m ) = 88.29 kN Summing moments at the base gives, ΣMbase = 0 Mmax - (88.29 kN)(1 m) = 0 Mmax = 88.29 kN-m |
|
| Section Modulus |
||
|
Now that the moment is known and the yield stress is given, the section modulus can be determined. There is a factor of safety of 3.0 that will reduce the allowable stress. Srequired = M/σ = 88.29 kN-m / (250,000/3 kN/m2 ) = 1,059 × 103 mm3 Looking at the appendix listing of all S type I-beams (note, SI units) give the lightest beam with at least 1,059 × 103 mm3 as S380 x 74 This beam type has a section modulus of 1,060 × 103 mm3 so it will just barely work. |
||
Practice Homework and Test problems now available in the 'Eng Mechanics' mobile app
Includes over 500 free problems with complete detailed solutions.
Available at the Google Play Store and Apple App Store.