| Ch 3. Beam Shear/Moment Diagrams | Multimedia Engineering Mechanics | ||||||
|
Shear and Moment |
Shear/Moment Diagrams |
Moving Loads |
|||||
| Moving Loads | Case Intro | Theory | Case Solution |
| Chapter |
| 1. Stress/Strain |
| 2. Torsion |
| 3. Beam Shr/Moment |
| 4. Beam Stresses |
| 5. Beam Deflections |
| 6. Beam-Advanced |
| 7. Stress Analysis |
| 8. Strain Analysis |
| 9. Columns |
| Appendix |
| Basic Math |
| Units |
| Basic Equations |
| Sections |
| Material Properties |
| Structural Shapes |
| Beam Equations |
| Search |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| Author(s): |
| Kurt Gramoll |
| ©Kurt Gramoll |
| MECHANICS - CASE STUDY SOLUTION |
||
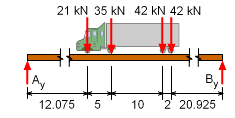
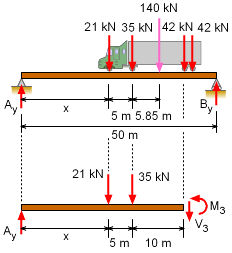
The fixed distances between the loads are determined by the wheel base of the vehicle but the location of the resultant force needs to be determined. Then the position of the truck where maximum bending moment will occur can be calculated. |
||
 Actual Wheel Force |
The total truck weight of 140 kN is distributed 15% on front wheels, 25 % on second wheels and remaining equally on third and fourth wheel. The actual load on each wheel is F1 = 15% of 140 kN = (140) (15) / 100 = 21 kN |
|
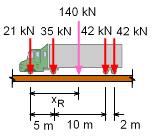 Resultant Force Location |
Since the load on each wheel is known, the resultant force position can be found by summing moments about the first wheel, giving ΣM1 = 0 The resultant force is located at 10.85 meters away from first wheel. |
|
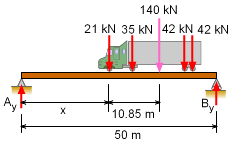 Beam Support Reaction |
The end reactions on the beam cannot be determined since the location of the truck is still unknown. However, the reactions can be modeled as a function of the truck location. Letting x represent the truck location, and summing the moments gives ΣMB= 0 One of the major difficulties in solving this type of problem is the maximum moment location is not known. However, since the bridge is simply supported, and the loads are all point force loads, the maximum moment will occur under one of the point loads. |
|
|
To help minimize the number of calculations, it can be further assumed that the maximum moment will not occur under the outside force loads since they are equal to or less than the inside two force loads. This means, only the second wheel and third wheel will be examined for the maximum bending moment. This assumption will be verified at the end of the problem. |
|
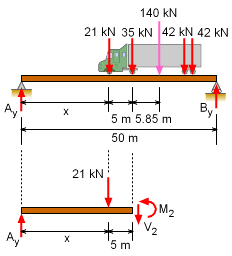 Location of Maximum Moment under Wheel 2 |
First, it is assumed that the maximum will occur at wheel 2 where the load is 35 kN. Cutting the beam at wheel two and summing moment at the cut, gives M2 = Ay (x + 5) - 21 (5) Remember, the truck can be at any location along the beam, and thus this equation needs to be maximized as a function of x. This gives, dM2/dx = 0 = 95.62 - 5.60 x Using this value of x, M2 becomes, M2 = 17.075 (95.62) - 2.80 (17.075)2 + 443.1 |
|
 Location of Maximum Moment Location of Maximum Moment under Wheel 3 |
Second, assume the maximum moment occurs at wheel 3. The moment is M3 = Ay (x + 15) - 21 (10 + 5) - 35 (10) Again, the truck can be at any location. The maximum will occur when, dM3/dx = 0 = 67.62 - 5.60 x Using this value of x, M3 becomes, M3 = -2.8 (12.075)2 + 67.62 (12.075) Comparing M2 and M3, bending moment is maximum under wheel 3 when wheel 1 is at 12.075 meters away from support A. |
|
|
|
For a complete understanding of the bending moment across the beam, a moment diagram can be constructed. Taking moments about support A and assuming counter clockwise (CCW) moment as positive gives, ΣMA= 0 Equating forces gives, ΣFy = 0 | |
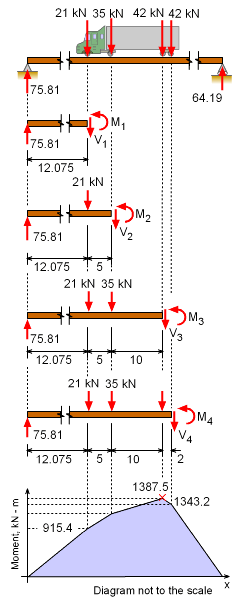 Final Moment Diagram |
Next, summing moment below each point load gives, M1 = 75.81 (12.075) M2 = 75.81 (12.075 + 5) - 21 (5) M3 = 75.81 (12.075 + 5 + 10) - 21 (5 + 10) M4 = 75.81 (12.075 + 5 + 10 + 2) Points A and B are supports so the bending moment at A and B is zero. As determined previous, the maximum bending moment occur under wheel 3 and will have a magnitude of 1,387.5 (kN-m) and it occurs when truck (first wheel) is at 12.075 meters away from support A. The moments under each wheel can be plotted to give the moment diagram, as shown on the left. Notice the bending moment under the first and fourth wheel is less than the maximum moment under the third wheel, as expected. Rarely is the maximum bending moment largest under one of the outside point loads. |
|
Practice Homework and Test problems now available in the 'Eng Mechanics' mobile app
Includes over 500 free problems with complete detailed solutions.
Available at the Google Play Store and Apple App Store.