| Ch 1. Stress and Strain | Multimedia Engineering Mechanics | ||||||
|
Normal Stress |
Shear and Bearing Stress |
Normal Strain |
Hooke's Law |
Thermal Effects |
Indeterminate Structures |
||
| Shear and Bearing Stress | Case Intro | Theory | Case Solution | Example |
| Chapter |
| 1. Stress/Strain |
| 2. Torsion |
| 3. Beam Shr/Moment |
| 4. Beam Stresses |
| 5. Beam Deflections |
| 6. Beam-Advanced |
| 7. Stress Analysis |
| 8. Strain Analysis |
| 9. Columns |
| Appendix |
| Basic Math |
| Units |
| Basic Mechanics Eqs |
| Sections |
| Material Properties |
| Structural Shapes |
| Beam Equations |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
|
|
||
|
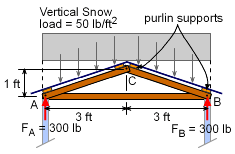
| The objective for this case is to determine
the shearing and bearing stress at joint A or B due to a 50 lb/ft2 snow
load on the roof of a small shed. |
|
| Truss Loading |
||
|
|
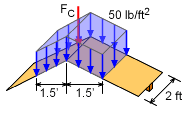
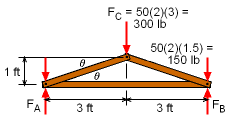
Since the structure and loading is symmetrical, joints A and B will be the same. This means, the reaction force from the wall at both joints will be equal, or FA = FB = (50 lb/ft2) (2 ft) (6 ft) / 2 = 300 lb Note that the truss spacing is 2 ft, so each truss must support a 2 ft wide section of roof loading. Also, only the vertical load is considered (50 lb/ft2) over the span of 6 ft. Next, the snow loading needs to be analyzed and replaced by equivalent force loads at the joints. The snow load on the plywood is supported by two purlins on each side of the roof. These purlins (one at the top and the bottom of each side) hold the trusses in place and transfer the roof load to the truss joints. The top purlins on each side of the roof will transfer only half of the roof load. The two bottom purlins will transfer the other half of the snow load. The load at the top center is FC = (50 lb/ft2)(2 ft)(1.5 ft + 1.5 ft) = 300 lb Half the load on each side of the roof is taken by the center purlins, so the center 3 ft width section of the roof is supported by the center joint. The remaining snow load on the roof is transferred to joints A and B. The roof angle is θ = tan-1 (1/3) = 18.43o |
|
| Member Loads |
||
|
|
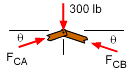
Before the bearing and shear stress at joint B can be determined, the force in member CB must be determined. This can be done by analyzing the top joint, C using static equilibrium equations, ΣFx
= 0 ΣFy =
0 |
|
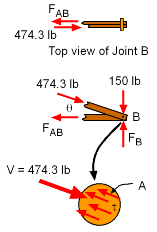 Shear Stress in Dowel from Member CB |
Shear Stress in Dowel |
|
The shear stress in the dowel pin at joint B is determined from the shear stress equation, τ = V/A The load in member FAB ( = 474 cos18.4 = 450 lb) will also cause a shear stress in the dowel, but since the load is less than the load in member FCB, the shear stress will also be lower. |
||
| Bearing Stress in Member AB |
||
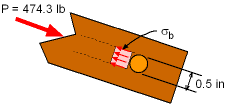 Bearing Stress in Member CB at Joint B |
The load in member AB is transferred into joint B through the dowel. This causes a bearing stress on the surface of the dowel against the member. The bearing stress is found by σb = P/Ab |
|
Practice Homework and Test problems now available in the 'Eng Mechanics' mobile app
Includes over 500 free problems with complete detailed solutions.
Available at the Google Play Store and Apple App Store.