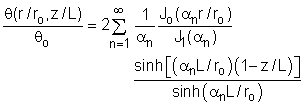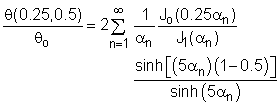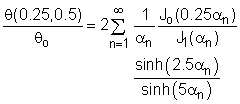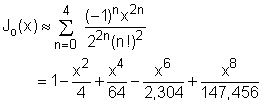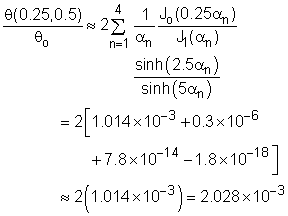| Ch 12. Infinite Sequences and Series | Multimedia Engineering Math | ||||||
|
Sequences and Series |
Integral and Comparison |
Alt. Series & Abs. Conv. |
Power Series |
Taylor, Mac. & Binomial |
|||
| Power Series | Case Intro | Theory | Case Solution |
| Chapter |
| 1. Limits |
| 2. Derivatives I |
| 3. Derivatives II |
| 4. Mean Value |
| 5. Curve Sketching |
| 6. Integrals |
| 7. Inverse Functions |
| 8. Integration Tech. |
| 9. Integrate App. |
| 10. Parametric Eqs. |
| 11. Polar Coord. |
| 12. Series |
| Appendix |
| Basic Math |
| Units |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
|
|
||||||||||||||||||||||||||||||||
|
|
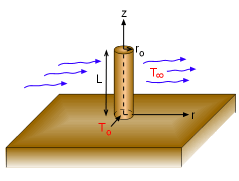
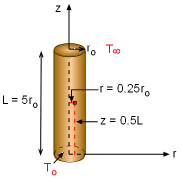
It is given that the two-dimensional steady-state temperature distribution of a circular fin is: For r/ro = 0.25, L/ro = 5, and z/L = 0.5, the above equation reduces to The next step is to determine the Bessel functions using five terms of the power series expansion: For α1 = 2.405, α2 = 5.520, α3 = 8.654, and α 4 = 11.792, the Bessel functions and hyperbolic sine functions are summarized in the following table:
|
|||||||||||||||||||||||||||||||
The dimensionless temperature at r/ro = 0.25, L/ro = 5, and z/L = 0.5 becomes Is the approximation for the Bessel functions good enough by only including five terms of the power series expansion? Use the simulation in this section to check the accuracy. Suppose that the first four zeros of Jo(α) are not given in the assumption, at least how many terms in the power series expansion do you need in order to obtain a reasonable solution? |
||||||||||||||||||||||||||||||||