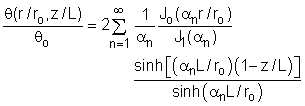| Ch 12. Infinite Sequences and Series | Multimedia Engineering Math | ||||||
|
Sequences and Series |
Integral and Comparison |
Alt. Series & Abs. Conv. |
Power Series |
Taylor, Mac. & Binomial |
|||
| Power Series | Case Intro | Theory | Case Solution |
| Chapter |
| 1. Limits |
| 2. Derivatives I |
| 3. Derivatives II |
| 4. Mean Value |
| 5. Curve Sketching |
| 6. Integrals |
| 7. Inverse Functions |
| 8. Integration Tech. |
| 9. Integrate App. |
| 10. Parametric Eqs. |
| 11. Polar Coord. |
| 12. Series |
| Appendix |
| Basic Math |
| Units |
| eBooks |
| Dynamics |
| Fluids |
| Math |
| Mechanics |
| Statics |
| Thermodynamics |
| ©Kurt Gramoll |
| |
||
| Introduction |
||
|
|
Fins are often used as a medium to increase
heat transfer. Joseph, an engineer, is interested in using a circular
fin with radius ro and length L to cool a hot wall. The wall
temperature at the base of protruding fin is To. The fin is
cooled by a fluid stream at |
|
| Questions |
||
| Determine the value of θ/θo for
r/ro = 0.25, L/ro = 5, and z/L = 0.5. |
||
| Approach |
||
|
||